一文讀懂Schnorr簽名如何提升比特幣_ASH:HASH幣

在閱讀Blockstream撰寫的MuSig論文時，我一直在想象，這對于我一個比特幣用戶來說，到底意味著什么。我發現Schnorr簽名的一些特性實在是非常棒而且便利，但某一些特性則非常煩人。在這篇文章里，我希望能跟各位分享我的想法。不過，我們先快速回顧一下。橢圓曲線簽名算法

當前比特幣的所有權體系用的是ECDSA。在簽名一條消息m時，我們先哈希這條消息，得出一個哈希值，即z=hash(m)。我們也需要一個隨機數k。在這里，我們不希望信任隨機數生成器，所以我們通常使用RFC6979，基于我們所知的一個秘密值和我們要簽名的消息，計算出一個確定性的k。使用私鑰pk，我們可以為消息m生成一個簽名，簽名由兩個數組成：r和s=(z+r*pk)/k。然后，使用我們的公鑰P=pk*G，任何人都可以驗證我們的簽名，也就是檢查(z/s)×G+(r/s)×P的x坐標確為r。

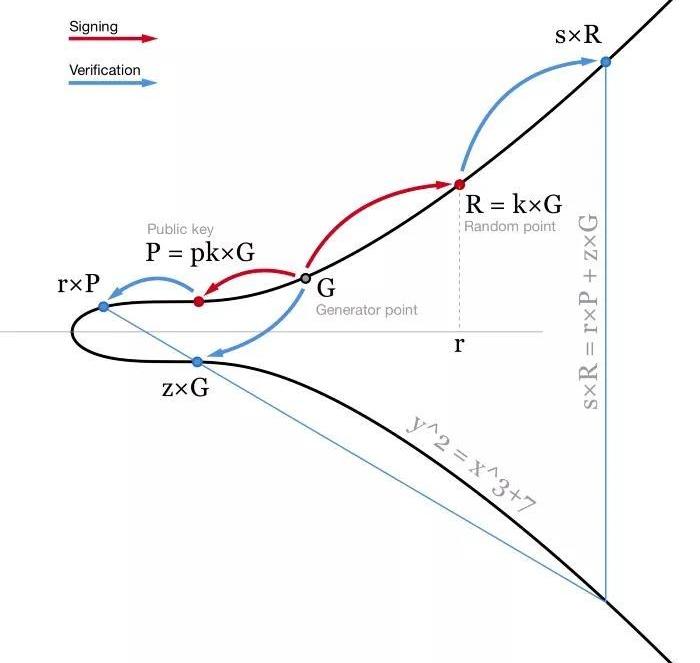
-ECDSA算法圖解。為便于說明，橢圓曲線作在實數域上-這種算法是很常見的，也非常好用。但還有提升空間。首先，簽名的驗證包含除法和兩次點乘法，而這些操作的計算量都非常大。在比特幣網絡中，每個節點都要驗證每一筆交易，所以當你在網絡中發出一筆交易時，全網幾千個節點都要驗證你的簽名。因此，即使簽名的過程開銷變得更大，讓驗證簽名變得更簡單也還是非常有好處的。其次，節點在驗證簽名時，每個簽名都要單獨驗證。在一個m-n的多簽交易中，節點必須多次驗證同一個簽名。比如一筆7-11的多簽名交易，里面包含了7個簽名，網絡中的每個節點都要分別驗證7個簽名。另外，這種交易的體積也非常大，用戶必須為此付出多得多的手續費。Schnorr簽名

Composable Finance推出跨鏈橋接“Centauri”:金色財經報道，波卡生態DeFi協議Composable Finance發推稱，其團隊已經在Polkadot和Kusama之間建立了一個去中心化跨鏈橋接“Centauri”。據稱，這是首個在Cosmos場景之外實現區塊鏈間通信（IBC）標準的產品。

新的非托管價值轉移工具允許在Kusama和Polkadot之間無縫和無需信任地轉移資金。在這一跨鏈橋的支持下，KSM/DOT、PICA/DOT和DOT/USDT流動性池由Composable Finance在Pablo DeFi上上線。目前，該產品和應用程序都處于公測階段，因此每種資產的上限為10000枚代幣。（U.Today）[2023/4/30 14:34:59]

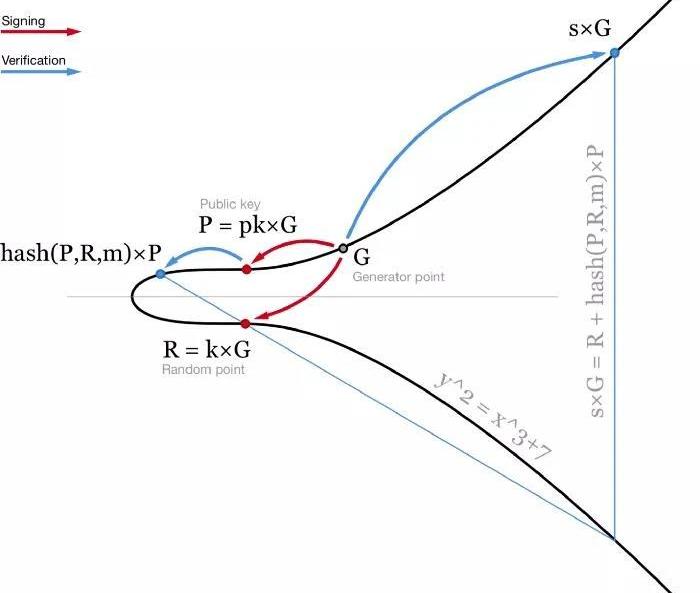
Schnorr簽名的生成方式有些許不同。它不是兩個標量(r,s)，而是一個點R和一個標量s。類似于ECDSA簽名，R是一個橢圓曲線上的隨機點R=k*G。而簽名的第二部分s的計算過程也有一些不同：s=k+hash(P,R,m)?pk。這里pk就是你的私鑰，而P=pk*G是你的公鑰，m就是那條消息。驗證過程是檢查s*G=R+hash(P,R,m)*P。

巨鯨從Crypto.com轉出2.5億枚DOGE，價值6300萬美元:2月16日消息，根據lookonchain鏈上監測，北京時間2月16日18:23:27，DOGE巨鯨地址「D7vrVR」從Crypto.com收到2.5億枚DOGE（約6300萬美元），現已成為Dogecoin前20名持有人之一，其地址余額為7.09億。昨日，該地址也從Crypto.com收到2億枚DOGE（約3900萬美元）。[2023/2/16 12:11:33]

-圖解Schnorr簽名和驗證-這個等式是線性的，所以多個等式可以相加相減而等號仍然成立。這給我們帶來了Schnorr簽名的多種良好特性。1.批量驗證

在驗證區塊鏈上的一個區塊時，我們需要驗證區塊中所有交易的簽名都是有效的。如果其中一個是無效的，無論是哪一個——我們都必須拒絕掉整個區塊。ECDSA的每一個簽名都必須專門驗證，意味著如果一個區塊中包含1000條簽名，那我們就需要計算1000次除法和2000次點乘法，總計約3000次繁重的運算。但有了Schnorr簽名，我們可以把所有的簽名驗證等式加起來并節省一些計算量。在一個包含1000筆交易的區塊中，我們可以驗證：(s1+s2+…+s1000)×G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)這里就是一連串的點加法和1001次點乘法。已經是幾乎3倍的性能提升了——驗證時只需為每個簽名付出一次重運算。

Coinbase將因Flare空投問題面臨集體訴訟:金色財經報道，根據向美國地方法院提起的訴訟，原告 Dallas Woody 已就 Coinbase 未能為其客戶提供 Songbird 和 Flare 代幣而對 Coinbase 提起集體訴訟。據稱加密貨幣交易所公開同意在 XRP 持有者之間分配空投。[2023/1/17 11:16:15]

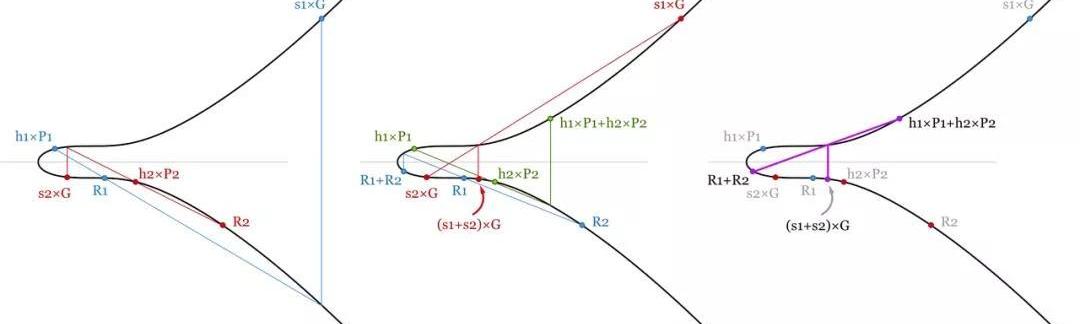
-兩個簽名的批量驗證。因為驗證等式是線性可加的，所以只要所有的簽名都是有效的，這幾個等式的和等式也必成立。我們節約了一些運算量，因為標量和點加法比點乘法容易計算得多。-2.密鑰生成

我們想要安全地保管自己的比特幣，所以我們可能會希望使用至少兩把不同的私鑰來控制比特幣。一個在筆記本電腦或者手機上使用，而另一個放在硬件錢包/冷錢包里面。即使其中一個泄露了，我們還是掌控著自己的比特幣。當前，實現這種錢包的做法是通過2-2的多簽名腳本。也就是一筆交易需要包含兩個獨立的簽名。有了Schnorr簽名，我們可以使用一對密鑰(pk1,pk2)，并使用一個共享公鑰P=P1+P2=pk1*G+pk2*G生成一個共同簽名。在生成簽名時，我們需要在兩個設備上分別生成一個隨機數，并以此生成兩個隨機點Ri=ki*G，再分別加上hash(P,R1+R2,m)，就可以獲得s1和s2了。最后，把它們都加起來即可獲得簽名(R,s)=(R1+R2,s1+s2)，這就是我們的共享簽名，可用共享公鑰來驗證。其他人根本無法看出這是不是一個聚合簽名，它跟一個普通的Schnorr簽名看起來沒有兩樣。不過，這種做法有三個問題。第一個問題是UI上的。要發起一筆交易，我們需要在兩個設備上發起多輪交互——為了計算共同的R，為了簽名。在兩把私鑰的情況下，只需訪問一次冷錢包：我們可以在熱錢包里準備好待簽名的交易，選好k1并生成R1=k1*G，然后把待簽名的交易和這些數據一同傳入冷錢包并簽名。因為已經有了R1，簽名交易在冷錢包中只需一輪就可以完成。從冷錢包中我們得到R2和s2，傳回給熱錢包。熱錢包使用前述的簽名交易，把兩個簽名加總起來即可向外廣播交易了。這在體驗上跟我們現在能做到的沒有什么區別，而且每當你加多一把私鑰，問題就會變得更加復雜。假設你有一筆財富是用10把私鑰共同控制的，而10把私鑰分別存放在世界各地，這時候你要發送交易，該有多麻煩！在當前的ECDSA算法中，每個設備你都只需要訪問一次，但如果你用上Schnorr的密鑰聚合，則需要兩次，以獲得所有的Ri并簽名。在這種情況下，可能不使用聚合，而使用各私鑰單獨簽名的方式會好一些——這樣就只需要一輪交互。文章完成后，我得到了ManuDrijvers的反饋：在一個可證明安全性的多簽名方案中，你需要3輪交互：選擇一個隨機數ki以及相應的隨機點Ri=ki\\G，然后告訴每一個設備Ri的哈希值ti=hash(Ri)，然后每個設備都能確保你沒有在知道其他人的隨機數之后改變主意*收集所有的數字Ri并計算公共的R簽名第二個問題是已知的Rogue密鑰攻擊。這篇論文講解得非常好，所以我就不贅述了。大概意思是如果你的其中一個設備被黑，并假裝自己的公鑰是，那就可以僅憑私鑰pk1便控制兩個私鑰共享的資金。一個簡單的解決方案是，在設置設備時，要求使用私鑰對相應的公鑰簽名。還有第三個重大問題。你沒法使用確定性的k來簽名。如果你使用了確定性的k，則只需一種簡單的攻擊，黑客即可獲得你的私鑰。攻擊如下：某個黑客黑入你的筆記本電腦，完全控制了其中一把私鑰。我們感覺資金仍是安全的，因為使用我們的比特幣需要pk1和pk2的聚合簽名。所以我們像往常一樣發起交易，準備好一筆待簽名的交易和R1，發送給我們的硬件錢包，硬件錢包簽名后將發回給熱錢包……然后，熱錢包出錯了，沒法完成簽名和廣播。于是我們再試一次，但這一次被黑的電腦用了另一個隨機數——R1'。我們在硬件錢包里簽名了同一筆交易，又將發回給了被黑的電腦。這一次，沒有下文了——我們所有的比特幣都不翼而飛了。在這次攻擊中，黑客獲得了同一筆交易的兩個有效的簽名：和。這個R2是一樣的，但是R=R1+R2和R'=R1'+R2是不同的。這就意味著黑客可以計算出我們的第二個私鑰：s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))?pk2或者說pk2=(s2-s2')/(hash(P,R1+R2,m)-hash(P,R1'+R2,m))。我發現這就是密鑰聚合最不方便的地方——我們每次都要使用一個好的隨機數生成器，這樣才能安全地聚合。3.Musig

巴塞爾委員會批準將于2025年實施的全球加密銀行規則:金色財經報道，根據周五的一份聲明，巴塞爾銀行監管委員會(BCBS)已批準其全球加密銀行規則，將于2025年1月1日實施。BCBS是銀行審慎監管的主要全球標準制定者，新規則建議銀行對某些加密資產的敞口不得超過2%，通常應低于1%。這些特定資產是代幣化的傳統資產，包括NFT、穩定幣和不符合分類條件的無擔保加密資產。此外，清單中確實符合標準的資產“根據現有巴塞爾框架中規定的基礎風險權重的資本要求”。BCBS設定的分類條件包括確保加密貨幣通過贖回風險測試和基礎風險測試，報告稱，贖回風險測試是為了確保儲備資產足以使加密資產隨時可贖回，基礎風險測試旨在確保加密資產的持有人能夠在市場上以合理的錨定價值出售。[2022/12/17 21:50:13]

MuSig解決了其中一個問題——roguekey攻擊將不能再奏效。這里的目標是把多方/多個設置的簽名和公鑰聚合在一起，但又無需你證明自己具有與這些公鑰相對應的私鑰。聚合簽名對應著聚合公鑰。但在MuSig中，我們不是把所有聯合簽名者的公鑰直接相加，而是都乘以一些參數，使得聚合公鑰P=hash(L,P1)×P1+…+hash(L,Pn)×Pn。在這里，L=hash(P1,…,Pn)——這個公共數基于所有的公鑰。L的非線性特性阻止了攻擊者構造特殊的公鑰來發動攻擊。即使攻擊者知道他的hash(L,Patk)×Patk應該是什么，他也無法從中推導出Patk來——這就跟你想從公鑰中推導出私鑰是一樣的。簽名構造的其它過程跟上面介紹的很像。在生成簽名時，每個聯合簽名者都選擇一個隨機數ki并與他人分享Ri=ki*G。然后他們把所有的隨機點加起來獲得R=R1+…+Rn，然后生成簽名si=ki+hash(P,R,m)?hash(L,Pi)?pki。因此，聚合簽名是(R,s)=(R1+…+Rn,s1+…+sn)，而驗證簽名的方法與以前一樣：s×G=R+hash(P,R,m)×P。4.默克爾樹多簽名

美聯儲卡什卡利：FOMC距離控制通脹“還有很長的路要走”:金色財經消息，美國明尼阿波利斯聯邦儲備銀行行長尼爾·卡什卡利（Neel Kashkari）周五表示，市場已經過分地預期央行將很快開始退縮。他在接受采訪時表示：“我對市場的解讀感到驚訝……聯邦公開市場委員會（FOMC）決心要把通脹率拉回到2％，我認為我們將繼續這么做，直至確信通脹率走上朝向2％的軌道，現在我們還有很長一段路。”（紐約時報）[2022/7/30 2:47:40]

你可能也注意到了，MuSig和密鑰聚合需要*所有簽名者簽名一個交易*。但如果你想做的是2-3的多簽名腳本呢？這時候我們能夠使用簽名聚合嗎，還是不得不使用通常的OP_CHECKMULTISIG和分別簽名？先說答案，是可以的，但是協議上將有些許的不同。我們可以開發一個類似于OP_CHECKMULTISIG的操作碼，只不過是檢查聚合簽名是否對應于公鑰默克爾樹上的一個元素。舉個例子，如果我們想用公鑰P1、P2和P3組成一個2-3的多簽名腳本，我們需要用這幾把公鑰的所有兩兩組合、、來構建一棵默克爾樹，并把默克爾樹根公布在鎖定腳本中。在花費比特幣時，我們需要提交一個簽名和一個證據，證明這個簽名所對應的公鑰位于由這個樹根標記的默克爾樹上。對于2-3多簽名合約來說，樹上只有3個元素，證據只需2條哈希值——那個我們想用的公鑰組合的哈希值，還有一個鄰居的。對于7-11多簽名腳本來說，公鑰組合有11!/7!/4!=330種，證據需要8條哈希值。通常來說，證據所包含的元素數量與多簽名的密鑰數量大體成正比，為log2(n!/m!/(n-m))。但有了默克爾公鑰樹，我們就不必局限于m-n多簽名腳本了。我們可以做一棵使用任意公鑰組合的樹。舉個例子，如果我們有一個筆記本電腦，一個手機，一個硬件錢包和一個助記詞，我們可以構建一棵默克爾樹，允許我們使用筆記本電腦+硬件錢包、手機+硬件錢包或者單獨的助記詞來使用比特幣。這是當前的OP_CHECKMULTISIG做不到的——除非你使用“IF-Else”式的流程控制來構造更復雜的腳本。

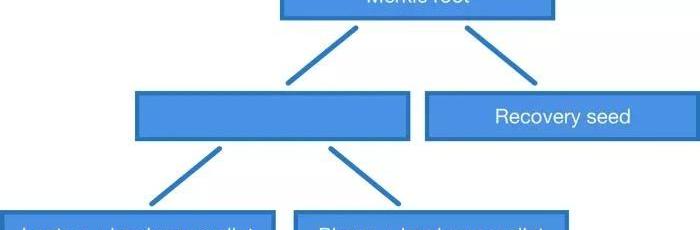
-聚合公鑰的默克爾樹。不僅僅是多簽名-結論

Schnorr簽名很棒，它解決了區塊驗證中的一些計算開銷問題，也給了我們密鑰聚合的能力。后者在使用時有些不便利，但我們不是在強迫大家使用它——無論如何，我們都可以仍舊使用普通的多簽名方案，使用單獨的、不聚合的簽名。我迫不及待想使用Schnorr簽名，希望比特幣協議能盡快納入這種簽名方案。另外，我也真心喜歡MuSig，它是個優雅的方案，論文也淺顯易懂。我強烈建議各位有閑之時通讀全文。

Tags：ASHHASHSCH比特幣Panda CashHASH幣pccschain波場幣和比特幣的區別是什么

波場