一文盤點主流ZKP實現方案特點_ZKP:PRO

原文：《慢霧：盤點 ZKP 主流實現方案技術特點》

作者：慢霧安全團隊

本文將為大家盤點各種 ZKP 實現的技術特點，希望能給大家的學習研究和工程開發帶來幫助。

在研究區塊鏈系統的工作原理時，我們需要了解各種各樣密碼學知識，比如 secp256k1，它是一種曲線和非對稱簽名算法，在比特幣和以太坊系統中用于簽名和驗證賬號。比如 sha256，它是一種哈希算法，用于把變長信息壓縮成定長編碼。比如 base58，它可以把信息編碼轉換成可打印字符表示的字符串。比如 ECDH，它是一種 Diffie - Hellman 密鑰交換算法，用于在 P2P 節點間安全交換通訊密鑰。

零知識證明（Zero-knowledge Proof）也是一種密碼學算法，簡稱為 ZKP 或者 ZK，它的特點是可以在不泄露任何其他信息的前提下證明一個命題的正確性（不少人對零知識證明這個名稱提出異議，認為“零泄露證明”更能代表它的本質能力）。

ZKP 最早在 1985 年就已經被提出，然而長期以來一直沒有找到大規模應用的場景，所以技術的發展也十分緩慢。一直到 2009 年比特幣誕生后，人們發現它非常適合用于解決區塊鏈中的隱私和擴展性問題，至此大量的資本和人才投入到了這項技術的開發和工程應用中。ZKP 有很多實現，例如：Groth16、PlonK、STARK 等，至今還沒出現真正的行業標準，本文將為大家盤點各種 ZKP 實現的技術特點，希望能給大家的學習研究和工程開發帶來幫助。

1. 隱私證明

Zcash 可能是 ZKP 的第一個被廣泛使用的應用，它在比特幣源代碼的基礎上，將 ZKP 應用于代幣的轉移，使得交易的信息完全保密，但同時能被區塊鏈上的節點驗證。

Tornado Cash 是在以太坊運行的混幣器，它使用 ZKP 證明 Merkle-Tree 上的節點，用戶可以將固定金額的代幣存入資金池，然后使用 ZKP 生成的 Proof 證明自己曾經存入過資金，但不需要暴露自己存入時的交易信息。

2. 計算外包

在區塊鏈中，每個節點的計算能力有限，但借助 ZKP 技術，節點可以將大量的計算外包給鏈下節點，這時只需要驗證外包提交的計算結果和計算證明就可以知道計算是否正確。

zksync1.0 就是一個很好的例子，它在鏈下進行以太坊代幣轉賬和交易，然后將結果提交給節點，節點通過驗證 ZKP 證明就可以知道它是否按照它聲明的方法進行計算。

Threshold Network與Immunefi合作推出高達50萬美元的漏洞賞金計劃:金色財經報道，隱私協議Threshold Network與漏洞賞金平臺Immunefi合作推出一項新的漏洞賞金計劃，以提高Threshold Network的安全性。該計劃提供高達50萬美元的獎勵，激勵“白帽”黑客識別和報告網絡協議和智能合約中的潛在漏洞。[2023/4/29 14:33:51]

3. 數據壓縮

Filecoin 運用 ZKP 構造了時空證明系統，能證明用戶在本地存儲了特定文件，目前已經證明存儲的文件已經達到 18 EiB。

Mina 是另一個例子，在很多高速區塊鏈系統中，交易的數據十分龐大，系統需要保留所有的區塊以備共識協議的驗證，所以系統對硬件的要求極高，永久保存意味著區塊鏈節點將需要不斷增大磁盤空間和數據索引能力。這時候可以借助 ZKP，將驗證數據壓縮，Mina 通過遞歸零知識證明，將賬本壓縮到 11 KB，但依舊可以驗證區塊的正確性。

證明系統是 ZKP 的底層算法實現，可分為交互式和非交互式兩種：

1. 交互式證明系統

交互證明系統由兩方參與，分別稱為證明者（Prover，簡記為 P）和驗證者（Verifier，簡記為 V），其中 P 知道某一秘密（如公鑰密碼體制的秘密鑰或一個二次剩余 x 的平方根），P 希望使 V 相信自己的確掌握這一秘密。交互證明由若干輪組成，在每一輪，P 和 V 可能需根據從對方收到的消息和自己計算的某個結果向對方發送消息。比較典型的方式是在每輪 V 都向 P 發出一個詢問，P 向 V 做出一個應答。所有輪執行完后， V 根據 P 是否在每一輪對自己發出的詢問都能正確應答，決定是否接受 P 的證明。

2. 非交互式證明系統

在上述交互式證明系統中，P 和 V 不進行交互，證明由 P 產生后直接給 V，V 對證明直接進行驗證，這種證明系統稱為非交互式證明系統（NIZK）。

我們在區塊鏈中使用的證明系統一般都是 NIZK，區塊鏈中的節點就是驗證者 V ，終端用戶或者二層網絡（Layer2）就是證明者 P。

文末參考鏈接  描述了近十年來公開發表的 NIZK 方案及特點。

在實際工程應用中我們主要關注的是性能和通用性，因此我們對一些常見證明系統進行更細致的分類對比，見文末參考鏈接 ：

巴西阿根廷商量欲推共同貨幣 以促進地區貿易、減少對美元依賴:金色財經報道，英國《金融時報》22日援引知情官員的話報道，巴西和阿根廷預計本周宣布就創建共同貨幣啟動準備工作，以促進地區貿易、減少對美元依賴。按照設想，巴西和阿根廷兩國創建共同貨幣，后續還會邀請其他拉美國家加入。[2023/1/23 11:26:51]

Bulletproofs

特點：簡潔證明大小，無需可信設置，但證明生成和驗證耗時相比較長。

代表項目：Bulletproofs, Halo, Halo2。

SNARKs (Succinct Non-interactive ARguments of Knowledge)

特點：簡潔證明大小，證明驗證耗時相比較短，但需要對每一個電路進行可信設置。

代表項目：Groth16。

SNORKs (Succinct Non-interactive Oecumenical (Universal) aRguments of Knowledge)

特點：簡潔證明大小，只需要進行一次可信設置即可用于所有電路。

代表項目：Sonic, PlonK, Marlin, Plonky2。

STARKs (Succinct (Scalable) Transparent ARguments of Knowledge)

特點：證明十分龐大，不需要進行可信設置，具有良好的可擴展性。

代表項目：STARK。

以上分類也不是絕對的，比如 Halo/Halo2 項目，它們在設計時也借鑒了很多 Plonk 的思路，另外，SNORKs 通常會被歸入到 SNARKs，因為它們都需要可信設置。

3. 性能對比

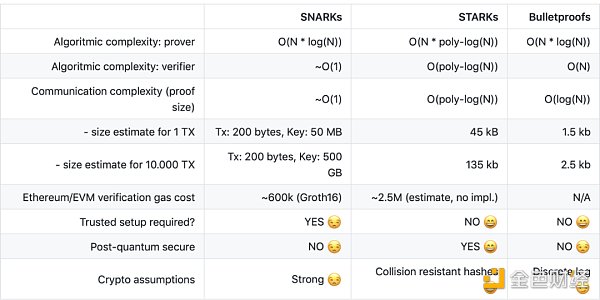
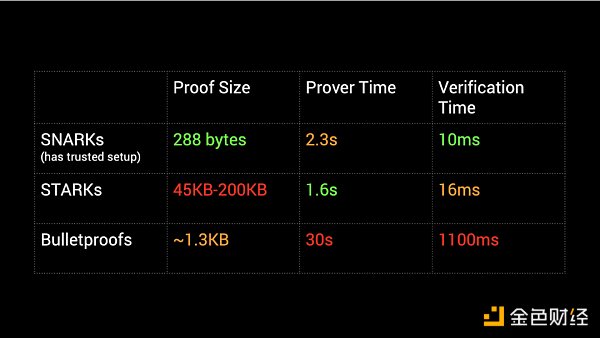
電路是 ZKP 系統的業務邏輯實現，開發 ZKP 應用需要進行電路編程，為什么 ZKP 邏輯代碼被稱為“電路”？主要有以下幾個原因：

穆長春：多邊央行數字貨幣橋可實現不同央行數字貨幣間互聯互通:金色財經報道，中國人民銀行數字貨幣研究所所長穆長春今日在2022香港金融科技周上表示，多邊央行數字貨幣橋項目利用金融科技手段，充分復用現有基礎設施，實現不同央行數字貨幣系統間及其與傳統金融市場基礎設施間的互聯互通。

穆長春介紹，央行數字貨幣應用于跨境場景需要考慮各司法管轄區不同監管要求和技術標準異構性。貨幣橋在業務設計之初就建立了基礎設施對接模塊，可兼容多種對接模式，包括跨境收付雙方均有各自的CBDC系統，或其中一方尚未建成法定數字貨幣（CBDC）系統等。因此，擁有本國央行數字貨幣系統不是參與貨幣橋項目的先決條件。[2022/11/1 12:05:34]

ZKP 證明的代碼會被轉換成一系列簡單約束條件的表達式 R1CS，然后使用拉格朗日插值法，轉換為一個巨大的多項式 QAP，最終以門電路的形式被約束。

與硬件電路類似，所有分支的代碼將被一起執行。

與硬件電路類似，ZKP 證明電路中沒有遞歸和復雜的循環，循環的數量只能是恒定的。

我們不需要從頭去用密碼學實現 ZKP 應用，有很多開發庫已經實現了這些底層證明系統，我們只需要關注業務邏輯的實現。當然每一種庫都有不同的抽象程度，有的需要去學習描述電路的表達式，有的只需要按流程定義好代碼就可以輕松實現。

1. 常用開發庫

libsnark

用 C++ 語言實現了通用證明系統、基礎電路庫和應用示例。

證明系統：BBFR15、BCCT12、BCCT13、BCGTV13、BCIOP13、BCTV14a、BCTV14b、CTV15、DFGK14、Groth16、GM17、GGPR13、PGHR13。

鏈接：https://github.com/scipr-lab/libsnark。

gnark

用 Go 語言實現的證明系統，提供高級 API 來設計電路。

證明系統：Groth16 、PlonK。

鏈接：https://github.com/consensys/gnark。

bellman

Rust 實現的證明系統，它提供電路接口、 基礎結構以及一些基本電路實現，例如布爾和數值抽象。

TokenPocket官網遭受異常流量攻擊，正緊急維護:10月11日，據官方公告，TokenPocket 官網遭受異常流量攻擊，技術團隊正在進行緊急維護。技術維護期間，TokenPocket 網站將不能正常訪問，用戶資產安全不會受到影響。官方提醒用戶提高警惕，注意識別欺詐風險。[2022/10/11 10:31:06]

證明系統：Groth16。

鏈接：https://github.com/zkcrypto/bellman。

snarkjs

Javascript 和 WASM 實現的證明系統，可用于可信設置、生成證明并驗證證明。snarkjs 使用 iden3 自己的 circom 編譯器對 DSL 定義的電路進行編譯。

鏈接：https://github.com/iden3/snarkjs。

ethsnarks

使用 Python 實現，可以在用戶瀏覽器生成證明，使用以太坊智能合約做為驗證者。目前項目開發不活躍，相同的場景下使用 Circom 可能是更好的選擇。

鏈接：https://github.com/HarryR/ethsnarks。

bulletproofs

使用 Rust 實現的證明系統，具有單一和聚合范圍證明、強類型多方計算，正在開發中用于證明任意語句的可編程約束系統 API。

證明系統：bulletproofs。

鏈接：https://github.com/dalek-cryptography/bulletproofs。

halo2

一個基于 Rust 的實現的證明系統，由 ZCash 團隊維護。Halo2 特定于 PLONKish，可以非常直接地控制電路在算術運算中的表示方式，非常適合編寫高度優化的電路。

證明系統：Halo2。

鏈接：https://github.com/zcash/halo2。

2. 開發流程

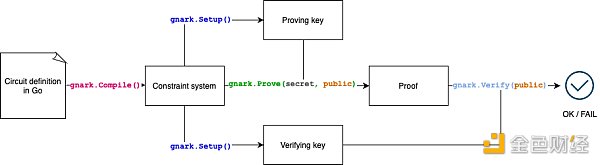
以 gnark 為例，一個典型的工作流程如下圖：

全球奢侈護膚品牌萊珀妮La Prairie發行首個NFT藝術收藏系列“Space Beyond”:金色財經報道，全球奢侈護膚品牌萊珀妮La Prairie發行首個NFT藝術收藏系列“Space Beyond”，

該NFT系列由數字藝術家 Carla Chan 設計，包含 365 + 1 個版本，NFT 根據天氣和人口數據實時生成，代表全球 31 個人口最多的城市一年中的一天。據悉，本次發行的 NFT 收益將用于保護世界各地的冰川。[2022/5/18 3:25:16]

1）用代碼描述需要解決的問題。

2）編譯成 R1CS 約束系統。

3）對 R1CS 進行可信設置，得到 Proving key 和 Verify key。

4）證明者使用 R1CS 和 Proving key 計算私密數據，生成證明 Proof。

5）驗證者使用 Verify key 驗證 Proof。

1. 基于以太坊平臺

Cairo

Cairo 是一種用于編寫可證明程序的編程語言，其中一方可以向另一方證明某個計算已正確執行。Cairo 和類似的證明系統可用于為區塊鏈提供可擴展性。StarkNet 將 Cairo 編程語言用于其基礎設施和編寫 StarkNet 合約。

證明系統：STARK。

鏈接：https://www.cairo-lang.org/docs/。

Zokrates

ZoKrates 采用 DSL 描述電路，提供了一些常用的電路庫，它可以幫助你在 DApp 中使用可驗證的計算，從用高級語言規范您的程序到生成計算證明，再到在 Solidity 中驗證這些證明。

證明系統：GM17、Groth16、Marlin。

鏈接：https://zokrates.github.io/。

Circom 語言采用 DSL 描述電路，可以配合 snarkjs 在用戶瀏覽器生成證明，使用以太坊智能合約做為驗證者。

鏈接：https://iden3.io/circom。

Noir

Aztec 基于 Rust 的隱私編程語言，采用 DSL 描述電路，允許安全、無縫地構建隱私保護零知識電路。

證明系統：PlonK。

鏈接：https://noir-lang.org/index.html。

zkEVM

與 EVM 一樣，zkEVM 是一個虛擬機，它作為程序操作的結果在狀態之間轉換，但是 zkEVM 通過生成證明來證明計算的每個部分的正確性。本質上，zkEVM 使用一種機制來證明執行步驟遵循規則。

目前有 zkSync、Polygon、Scroll、Starkware 等團隊正致力于 zkEVM 的實現，已取得重大進展。

2. 基于公鏈平臺

zkApp (Mina)

zkApps 是 Mina Protocol 的智能合約，由零知識證明提供支持。zkApps 可以在鏈下執行任意復雜的計算，同時只收取固定費用以將生成的零知識證明發送到鏈以驗證此計算，這與其他在鏈上運行計算并使用基于可變 gas 費用的區塊鏈相反模型。zkApps 使用 Typescript 編寫。

鏈接：https://docs.minaprotocol.com/zkapps。

LEO (Aleo)

Leo 是一種函數式靜態類型編程語言，專為編寫私有應用程序而構建。它專為開發人員設計，可以直觀地在 Aleo 區塊鏈上構建，為私有的、去中心化的生態系統提供基礎。

證明系統：Marlin。

鏈接：https://leo-lang.org/。

在過去幾年，慢霧安全團隊已為多個知名 ZKP 產品進行了電路及應用安全審計，包括 ZKSwap、Zkdex、Zksafe 等，發現了多個中高危漏洞，對基于 Circom、libsnark 等流行框架開發的應用有較為深入的理解。慢霧安全團隊在 ZKP 應用審計中發現常見的安全問題有：

信任參數風險

為了使用 zk-SNARKs，需要一組公共參數，稱為公共參考字符串（CRS）。但是這些參數的創建也會產生一些私有參數，如果某一方獲得這些私有參數，他們就可以偽造證明。

另外，生成 CRS 的流程需要經過審計，確保不會有隨機數后門，或者私有參數不會被蓄意保留。使用 zk-SNORKs 時也需要確保結構化參考字符串（SRS）是可信的。

可信配置階段的安全隱患問題可以使用安全多方計算（MPC）來解決，MPC 的特點是只要任何一個參與者能誠實參與，那么通過這套多方計算系統最終得到的計算結果就是可信的。

靜態代碼安全

這部分主要是由于編碼不規范造成的安全問題，例如：參數未校驗、返回值未處理、數值溢出、邊界未檢查等，如果編寫電路的語言是 C/C++，那么還會存在內存溢出風險。

供應鏈攻擊風險

供應鏈的風險主要來自使用了存在漏洞的代碼庫，例如：舊版本的倉庫。通常 ZKP 應用還需要配合客戶端或者 Web 前端使用，而這部分也很容易遭受多種方式黑客攻擊。

邏輯錯誤

邏輯錯誤是電路實現中最容易出現的錯誤，需要結合需求文檔檢查電路的設計是否符合需求。

雙花攻擊

錯誤的設計可能導致雙花攻擊，例如：某些 ZKP 庫存在延展性風險，攻擊者可利用已知的 Proof 生成不同 Proof，如果設計不當會導致雙花攻擊。

證明偽造

有效的證明是 ZKP 首要解決的問題，確保滿足完備性和可靠性，即“假的真不了，真的假不了”，所以如果一個電路可以創建假證明，通常是由于底層庫出現漏洞，通常我們會建議項目方使用公開的經過審計的 ZKP 庫，并使用穩定的發行版。

側信道攻擊

如果電路設計不當，不同的隱私信息可能存在不同的計算特征，攻擊者可能通過公開的輸入或者證明猜解出私有輸入數據。

電路約束失效

不恰當的電路表達式可能導致變量未被約束。

特殊值攻擊

一些特殊的輸入值可能繞過系統的驗證邏輯，例如：0、null 等。

隱私輸入猜解

對于 Tornado Cash 等應用，如果輸入的信息可以被猜解，那么會導致嚴重的隱私泄露問題，這時需要對輸入數據進行嚴格審計，確保不能被猜解。

RugPull 風險

一些項目可能存在特殊的管理員權限，一旦權限被非法使用會導致項目資金和用戶資產被竊取。

智能合約風險

一些 ZKP 證明使用智能合約進行驗證，例如：Circom、ZoKrates 等。智能合約可能出現重入、重放、邏輯錯誤等風險，詳情可查看慢霧安全團隊的智能合約安全審計服務。

針對上面列舉的 ZKP 安全問題，慢霧安全團隊在攻防實戰中總結出了一套安全解決方案，結合黑盒/灰盒/白盒多種測試手段，推出了面向區塊鏈行業的 ZKP 電路審計服務。

零知識證明是解決區塊鏈隱私性、計算擴展和數據壓縮問題的有效方法，目前有很多的實現方案，這些實現方案具有不同的性能參數指標和安全基準。開發者在開發零知識證明電路時需要注意根據需求選擇合適的框架，并確保在項目上線前對應用的安全性進行過全面安全審計。

最后，感謝領先的一站式數字資產自托管服務商 Safeheron 提供的專業技術建議。

參考鏈接：

. https://en.wikipedia.org/wiki/Zero-knowledge_proof

. https://github.com/matter-labs/awesome-zero-knowledge-proofs

. https://docs.google.com/presentation/d/1gfB6WZMvM9mmDKofFibIgsyYShdf0RV_Y8TLz3k1Ls0/edit

慢霧科技

個人專欄

閱讀更多

金色早8點

金色財經

Odaily星球日報

歐科云鏈

澎湃新聞

Arcane Labs

深潮TechFlow

MarsBit

BTCStudy

鏈得得

Tags：ZKPARKPROCOMzkProofDARK價格Meblox ProtocolComPro

pepe最新價格