科普之密碼專欄 | 動手計算雙線性對（中）_區塊鏈:USD

前言

上一篇分享了“模運算”相關的知識，并且計算了一些有限域的例子，這一篇我們討論在通用零知識證明中經常提到的橢圓曲線和雙線性配對。橢圓曲線作為雙線性對的基礎和前置知識，我們首先介紹一下其在實數域上的表現形式，然后通過計算的方法列出”F_101”和其擴域“F_101^2”上的全部元素的列表。

橢圓曲線相關知識---曲線方程

橢圓曲線的一般形式的方程其實比較復雜，稱為Weierstrass方程，形如下面的形式：

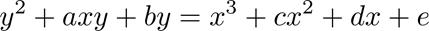
我們先將a,b,c,d,e隨意的取值為1,2,3,4,5，并通過畫圖來查看曲線在直角坐標系上的表現形式。根據二次方程求根公式，我們將其變換為x關于y的函數

穩定幣crvUSD科普創新清算機制LLAMMA，可在抵押品價格下跌時逐步替換為穩定幣:1月17日消息，Curve官方科普其穩定幣crvUSD創新的清算機制LLAMMA，解釋了LLAMMA通過AMM的特性進行針對債務人更友善的清算方式，讓抵押品在價格下跌時逐漸轉移成穩定幣，讓原本要清償的債務有一定程度的穩定幣可以償還，同時在價格回穩時再逐漸把穩定幣換回抵押品，而不是直接的觸發清算導致債務人的虧損。

此前報道，2022年11月23日，去中心化交易平臺CurveFinance開發者發布Curve即將推出的去中心化Stablecoin“crvUSD”的官方代碼和白皮書。[2023/1/17 11:17:13]

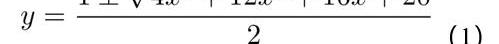
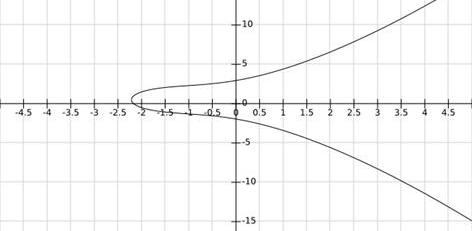
根據方程作圖如下：

國務院：推進科普與區塊鏈技術深度融合:為貫徹落實黨中央、國務院關于科普和科學素質建設的重要部署，依據《中華人民共和國科學技術進步法》、《中華人民共和國科學技術普及法》制定《全民科學素質行動規劃綱要（2021－2035年）》，其中要求實施智慧科普建設工程。推進科普與區塊鏈等技術深度融合，強化需求感知、用戶分層、情景應用理念，推動傳播方式、組織動員、運營服務等創新升級，加強“科普中國”建設，強化科普信息落地應用，與智慧教育、智慧城市、智慧社區等深度融合。（新華社）[2021/7/10 0:40:52]

根據上面的方程和作圖過程了解道，曲線由上下兩個半支組成，關于y=0.5對稱。

對稱的總是美的，但是這個曲線卻有一點瑕疵，他的對稱軸并不是x軸而是y=0.5。考慮到Weierstrass太過復雜，人們更經常使用的是在Weierstrass方程的基礎上進行一些坐標變換和參數化簡后的形式。新的形式關于x軸對稱。

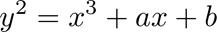
動態 | 新浪財經：官媒針對區塊鏈的報道從科普宣傳轉向打假監管:據新浪財經今日消息，“1025新政”滿月，一個月間，官媒對區塊鏈的態度風向已轉。據11月初的一項統計，七家黨媒在新政一周內發布了65篇直接相關報道，當時文章中的關鍵詞是數據、產業、安全、創新等，大量文章偏向于科普區塊鏈的概念以及應用介紹，提醒警惕虛擬貨幣炒作的僅有3篇。近期，官媒的批評焦點則紛紛指向借區塊鏈之名進行的虛擬貨幣發行和炒作行為。據統計，新華網、人民網收錄轉載的，以打擊虛擬貨幣或揭露假借區塊鏈行騙為主題的文章，自10月25日到11月25日午間，共28篇；其中，11月19日至11月25日的一周內就高達15篇。這些文章主要圍繞三個觀點展開：厘清區塊鏈和虛擬貨幣的關系，說明二者概念不等；打擊偽“區塊鏈”騙局，或是虛擬貨幣騙局揭露；提醒民眾，區塊鏈不能成為炒作的噱頭，更不是行騙的招牌，需警惕此類活動，理性投資。[2019/11/26]

當取a=0，b=3時，畫出曲線如下圖，容易驗證是曲線上一點，對稱的也是。

動態 | 人民日報官方微博科普區塊鏈 強調區塊鏈不等于比特幣:人民日報官方微博今早發表9圖科普區塊鏈。其中涉及區塊鏈的特點有：1、安全；2、不可篡改；3、可訪問；4、無第三方。區塊鏈對未來的影響：1、不需繁瑣個人證明；2、看病避免反復檢查；3、旅行消費更加便捷；4、交易無需第三方。同時強調，區塊鏈不等于比特幣。比特幣只是區塊鏈技術的一種應用，區塊鏈還有醫療衛生、食品安全、版權保護等諸多應用領域。[2019/10/28]

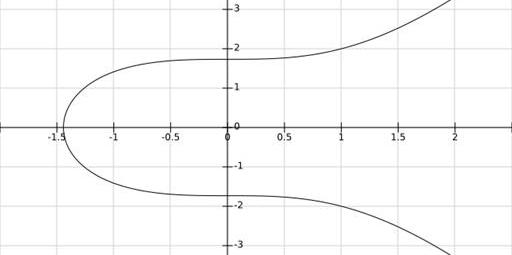
通過方程我們畫出了曲線y^2=x^3+3的圖像，但是說這就是橢圓曲線的圖像其實并不準確。準確地說，我們畫的是在實數域上這個方程的圖像。在復數域上當然有更多的點也滿足曲線方程但是我們的圖像中并沒有體現，例如。如果把曲線看作點的集合，那數域的擴張直接影響到我們要討論的這個集合的大小，這在本文后半部分我們還會看到。

聲音 | ETC Labs主管：科普教育是未來幾年公鏈面臨的巨大挑戰:ETCLabs主管Darin Kotalik認為，科普教育是未來幾年公鏈面臨的巨大挑戰，人們必須要對區塊鏈有基本的認識，分清楚公鏈和私鏈的區別。[2019/8/25]

另外為了讓其擁有更多的性質，我們認為橢圓曲線其實還包括一個“無窮遠”點。這個點在圖中并不能體現出來，我們也不能以直角坐標的形式寫出這個點的坐標，但是當我們說橢圓曲線時默認其點的集合中包含這個點。“無窮遠點”一般用"O?"表示。

橢圓曲線相關知識---點的運算

就像討論“F_7”時那樣，有了元素的集合還需要有在集合上的運算。這條曲線就是橢圓曲線點的集合，但是為了構建密碼算法還需要定義點的運算。不同于域中需要兩種基本運算，這里我們只需要定義一種特殊的基本運算就可以，不妨將這種運算稱作加法，用“+”表示。

通過幾何意義可以清楚的理解這種運算的定義，例如我們選取了曲線上的兩個點A和B計算加法，把A+B的結果記為C，過程如下：

1）過AB做直線，交曲線于T；

2）過T做x軸垂線，交曲線于C點，C即為所求；

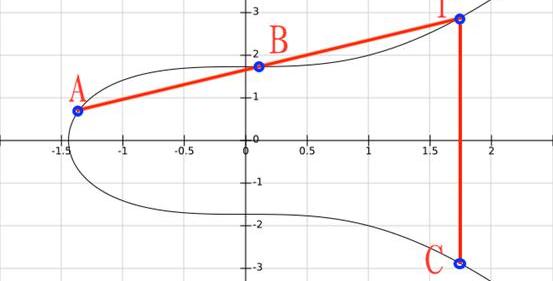
需要說明的是，當兩個“加數”位置的點為同一個點時，步驟一中所做的其實是過該點的切線。另外，當AB的連線本身就垂直于x軸時，我們規定AB和曲線的第三個交點是無窮遠點“O”。

在這樣的規則下容易發現，任何點P都有一個對應的P’,使得P+P’=O；并且任何點A和O的運算的結果都是A本身。而且因為連線AB和連線BA其實是同一條直線，因此我們也能夠得知這里定義的點的加法是滿足交換率的。

根據定義再結合一些解析幾何的知識，就可以求出點加法的坐標計算公式。例如假設A和B的坐標分別為(Xa,Yb)和(Xa,Yb),那么C點坐標如下：

其中"λ"是直線AB連線的斜率，或者當A、B重合時是A點的切線斜率。

現在我們將轉而討論有限域上的橢圓曲線，其上的橢圓曲線表現為一些散布的點。在有限域上A+B雖然已經沒有明確的幾何意義，但是有同樣的計算公式。我們已經驗證過是橢圓曲線上的點，那么我們就把該點記為G，并且從該點開始，計算G,G+G，G+G+G...看看會有怎樣的規律。

以G+G為例，我們進行演算,首先計算λ，也就是G點的斜率：

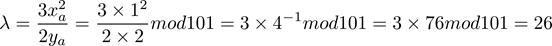
然后計算C點坐標：

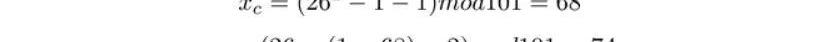
因此G+G的坐標為。而G+2G稍稍有不同，主要是λ需要從切線斜率修改為過AB的直線斜率：

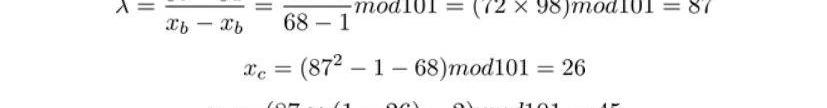
因此我們也計算出G+2G=3G的坐標，以此類推進行計算，我們得到下表

讀者可以選擇表中的點，例如(32,42)，來驗證其是否在曲線上，也就是是否滿足曲線方程y^2=x^3+3mod101，相關演算我們不在本文贅述。

經過計算和驗證可以發現，這一系列點構成了一個周期為17的循環。如果我們將k個G相加記為kG，并且將O看作0G，那么有17G=O。這像極了模17加法的規律，并且在模17加法和為0的兩個數對應的兩個橢圓曲線點的和正好是O，我們說這樣的17個點和加法一起構成一個有17個元素的循環群。因為這只是一篇科普性質的文章，我們不給出循環群的嚴格定義，但是正如它的名字中強調的“循環”，循環群最突出的性質就是能夠由某個元素不斷運算從而得到全部。

需要強調的是這17個點并不是F_101上橢圓曲線的全部，但僅利用這17個元素組成的集合我們已經能夠在其中完成點的加法運算，也就是說任意選擇集合中兩個點進行加法，其結果不會跳出到集合之外。

在本篇最后，我們展示17個點在直角坐標系中的分布，讀者可以體會其中的對稱之美。下一篇我們將找到另一個17個元素的循環群并且在其基礎上計算雙線性映射，敬請期待。

附錄

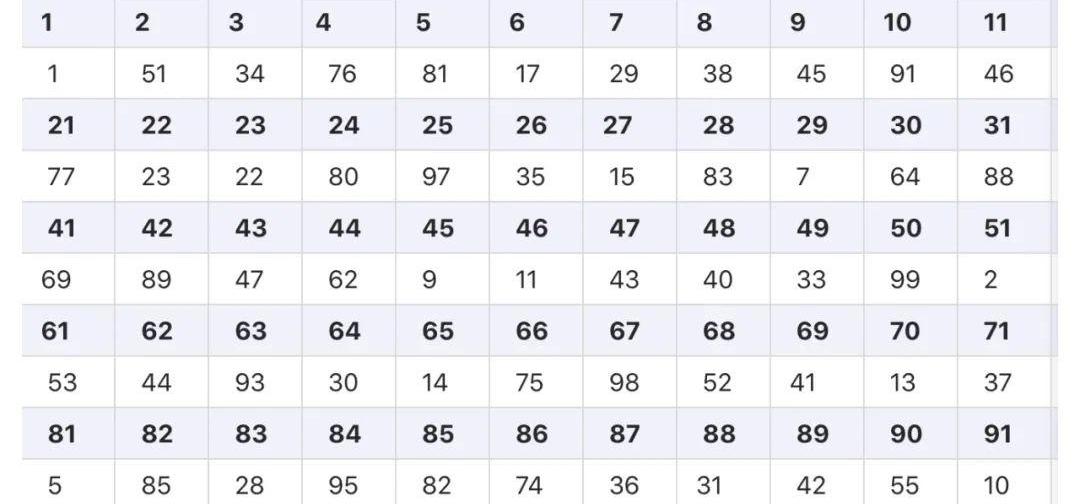
▲表2：模101元素逆元表

喬沛楊

趣鏈科技基礎平臺區塊鏈底層密碼學小組

Tags：區塊鏈穩定幣AMMUSD區塊鏈域名開發穩定幣是什么意思簡單AMM價格USDA

狗狗幣