隨機過程在數據科學和深度學習中有哪些應用？_ARM:ARM幣是什么幣ARMA幣

“Theonlysimpletruthisthatthereisnothingsimpleinthiscomplexuniverse.Everythingrelates.Everythingconnects”

—JohnnyRich,TheHumanScript

介紹

機器學習的主要應用之一是對隨機過程建模。機器學習中一些隨機過程的例子如下:

泊松過程:用于處理等待時間以及隊列。隨機漫步和布朗運動過程:用于交易算法。馬爾可夫決策過程:常用于計算生物學和強化學習。高斯過程:用于回歸和優化問題(如,超參數調優和自動機器學習)。自回歸和移動平均過程:用于時間序列分析(如,ARIMA模型)。在本文中，我將簡要地向你介紹這些隨機過程。

歷史背景

隨機過程是我們日常生活的一部分。隨機過程之所以如此特殊，是因為隨機過程依賴于模型的初始條件。在上個世紀，許多數學家，如龐加萊，洛倫茲和圖靈都被這個話題所吸引。

如今，這種行為被稱為確定性混沌，它與真正的隨機性有著截然不同的范圍界限。

由于愛德華·諾頓·洛倫茲的貢獻，混沌系統的研究在1963年取得了突破性進展。當時，洛倫茲正在研究如何改進天氣預報。洛倫茲在他的分析中注意到，即使是大氣中的微小擾動也能引起氣候變化。

洛倫茲用來描述這種狀態的一個著名的短語是:

“AbutterflyflappingitswingsinBrazilcanproduceatornadoinTexas”(在巴西，一只蝴蝶扇動翅膀就能在德克薩斯州制造龍卷風)—EdwardNortonLorenz(愛德華·諾頓·洛倫茲)

這就是為什么今天的混沌理論有時被稱為“蝴蝶效應”。

分形學

一個簡單的混沌系統的例子是分形(如圖所示)。分形是在不同尺度上不斷重復的一種模式。由于分形的縮放方式，分形不同于其他類型的幾何圖形。分形是遞歸驅動系統，能夠捕獲混沌行為。在現實生活中，分形的例子有:樹、河、云、貝殼等。

Chainlink 可驗證隨機函數 v2 上線主網:金色財經報道，區塊鏈預言機解決方案 Chainlink 宣布發布 Chainlink 可驗證隨機函數 v2。除了在以太坊主網上運行之外，Chainlink Network 還計劃部署到其他區塊鏈上，例如 Polygon 和 BNB。v2 的主要升級包括增強的訂閱管理、調整Gas限制的能力、擴展區塊確認以及能夠在單個鏈上交易中請求多個隨機數。與 v1 相比，新改進的版本可以將交易費用降低 60%。

報道稱，自推出以來，Chainlink VRF (v1) 已成為區塊鏈行業采用最廣泛的隨機數生成器解決方案，完成了超過 300 萬次請求交易，目前為多個區塊鏈網絡中的 2,200 多個獨特的智能合約提供可驗證的隨機性。Chainlink 聯合創始人 Sergey Nazarov 表示：“只有具有可驗證、防篡改的隨機性，才能安全地鑄造 NFT 及其屬性或確保基于區塊鏈的游戲的公平結果”。[2022/2/18 9:59:33]

圖1:MC.Escher，SmallerandSmaller

在藝術領域有很多自相似的圖形。毫無疑問，MC.Escher是最著名的藝術家之一，他的作品靈感來自數學。事實上，在他的畫中反復出現各種不可能的物體，如彭羅斯三角形和莫比烏斯帶。在"SmallerandSmaller"中，他也反復使用了自相似性(圖1)。除了蜥蜴的外環，畫中的內部圖案也是自相似性的。每重復一次，它就包含一個有一半尺度的復制圖案。

確定性和隨機性過程

有兩種主要的隨機過程:確定性和隨機性。

在確定性過程中，如果我們知道一系列事件的初始條件(起始點)，我們就可以預測該序列的下一步。相反，在隨機過程中，如果我們知道初始條件，我們不能完全確定接下來的步驟是什么。這是因為這個過程可能會以許多不同的方式演化。

SHAP按計劃對SHIB持倉用戶進行了隨機地址空投:據公開消息，BSC上社區自治型代幣SHAP（沙皮狗）已向以太坊上SHIB持幣地址進行了隨機空投。用戶在導入BSC賬戶后將收到SHAP獎勵。目前階段有700-1000個地址收到了空投獎勵。

SHAP沙皮狗項目開發已經進行了包括SHAP DAO社區和SHAP Shuttle 功能開發工作，多家交易所已加入SHAP白名單計劃。[2021/5/12 21:54:52]

在確定性過程中，所有后續步驟的概率都為1。另一方面，隨機性隨機過程的情況則不然。

任何完全隨機的東西對我們都沒有任何用處，除非我們能識別出其中的模式。在隨機過程中，每個單獨的事件都是隨機的，盡管可以識別出連接這些事件的隱藏模式。這樣，我們的隨機過程就被揭開了神秘的面紗，我們就能夠對未來的事件做出準確的預測。

為了用統計學的術語來描述隨機過程，我們可以給出以下定義:

觀測值:一次試驗的結果。總體:所有可能的觀測值，可以記為一個試驗。樣本:從獨立試驗中收集的一組結果。例如，拋一枚均勻硬幣是一個隨機過程，但由于大數定律，我們知道，如果進行大量的試驗，我們將得到大約相同數量的正面和反面。

大數定律指出:

“隨著樣本規模的增大，樣本的均值將更接近總體的均值或期望值。因此，當樣本容量趨于無窮時，樣本均值收斂于總體均值。重要的一點是樣本中的觀測必須是相互獨立的。”--JasonBrownlee

隨機過程的例子有股票市場和醫學數據，如血壓和腦電圖分析。

泊松過程

泊松過程用于對一系列離散事件建模，在這些事件中，我們知道不同事件發生的平均時間，但我們不知道這些事件確切在何時發生。

如果一個隨機過程能夠滿足以下條件，則可以認為它屬于泊松過程:

事件彼此獨立(如果一個事件發生，并不會影響另一個事件發生的概率)。兩個事件不能同時發生。事件的平均發生比率是恒定的。讓我們以停電為例。電力供應商可能會宣傳平均每10個月就會斷電一次，但我們不能準確地說出下一次斷電的時間。例如，如果發生了嚴重問題，可能會連續停電2-3天(如,讓公司需要對電源供應做一些調整)，以便在接下來的兩天繼續使用。

萊比特創始人江卓爾：加密貨幣市場是不可預測的，有一定的隨機性:12月23日，“瞰見未來—國際區塊鏈技術創新峰會暨Cointelegraph中文一周年”在三亞灣海居鉑爾曼酒店拉開序幕，本次大會由Cointelegraph中文主辦、Nova聯合主辦，匯聚重磅嘉賓、聚焦行業熱門議題，共討2020年區塊鏈技術發展、落地應用場景，展望區塊鏈行業的未來發展趨勢。

萊比特創始人江卓爾發表了個人主題演講《加密貨幣行業最困難的任務》。他表示，加密貨幣市場是不可預測的，它有一定的隨機性，沒有人可以預測短期的價格變化，所有的技術分析指標在短期內都是無意義的。對于多數人而言，挖礦是一個很好的選擇，可以把挖礦當做一個經營行為，而不是投資行為。一旦你開始挖礦，一定要把挖出來的幣屯下來，而不是把幣賣掉。[2020/12/23 16:17:01]

因此，對于這種類型的隨機過程，我們可以相當確定事件之間的平均時間，但它們是在隨機的間隔時間內發生的。

由泊松過程，我們可以得到一個泊松分布，它可以用來推導出不同事件發生之間的等待時間的概率，或者一個時間段內可能發生事件的數量。

泊松分布可以使用下面的公式來建模(圖2)，其中k表示一個時期內可能發生的事件的預期數量。

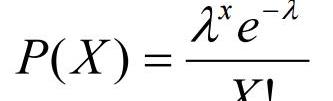
圖2:泊松分布公式

一些可以使用泊松過程模擬的現象的例子是原子的放射性衰變和股票市場分析。

隨機漫步和布朗運動過程

隨機漫步是可以在隨機方向上移動的任意離散步的序列(長度總是相同)(圖3)。隨機漫步可以發生在任何維度空間中(如:1D，2D，nD)。

動態 | EOS競猜游戲HiGold Game遭隨機數攻擊:今天中午，11:57至12:01之間，PeckShield安全盾風控平臺DAppShield監測到黑客向EOS競猜類游戲HiGold Game發起連續攻擊，已實現獲利。針對異常獲利情況，PeckShield安全人員隨即和項目方取得聯系，及時暫停了游戲合約，避免了進一步資產損失。PeckShield安全人員在此提醒，開發者應在合約上線前做好安全測試，特別是要排除已知攻擊手段的威脅，必要時可尋求第三方安全公司協助，幫助其完成合約上線前攻擊測試及基礎安全防御部署。[2019/7/3]

圖3:高維空間中的隨機漫步

現在我將用一維空間(數軸)向您介紹隨機漫步，這里解釋的這些概念也適用于更高維度。

我們假設我們在一個公園里，我們看到一只狗在尋找食物。它目前在數軸上的位置為0，它向左或向右移動找到食物的概率相等(圖4)。

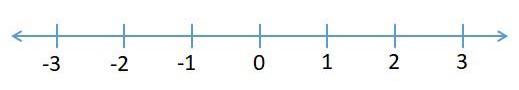
圖4:數軸

現在，如果我們想知道在N步之后狗的位置是多少，我們可以再次利用大數定律。利用這個定律，我們會發現當N趨于無窮時，我們的狗可能會回到它的起點。無論如何，此時這種情況并沒有多大用處。

因此，我們可以嘗試使用均方根(RMS)作為距離度量(首先對所有值求平方，然后計算它們的平均值，最后對結果求平方根)。這樣，所有的負數都變成正數，平均值不再等于零。

在這個例子中，使用RMS我們會發現，如果我們的狗走了100步，它平均會從原點移動10步(√100=10)。

如前面所述，隨機漫步用于描述離散時間過程。相反，布朗運動可以用來描述連續時間的隨機漫步。

隱馬爾科夫模型

Zcash開發人員利用切爾諾貝利核電站的核廢料來產生隨機數 :Zcash的開發人員在該網絡最新的秘密保證儀式中使用了切爾諾貝利核電站的核廢料。上個周末，Zcash的兩位開發人員舉行了他們最新的“Tau”儀式，并特別使用核廢料來產生隨機數。Andrew Miller表示，Tau的力量完全在于生成和安全地處理加密的“有廢物”，從理論上講，其結果是一個完全隨機的、私有的代碼，可以用來構建Zcash。[2018/1/28]

隱馬爾可夫模型都是關于認識序列信號的。它們在數據科學領域有大量應用，例如:

計算生物學。寫作/語音識別。自然語言處理(NLP)。強化學習HMMs是一種概率圖形模型，用于從一組可觀察狀態預測隱藏(未知)狀態序列。

這類模型遵循馬爾可夫過程假設:

“鑒于我們知道現在，所以未來是獨立于過去的"

因此，在處理隱馬爾可夫模型時，我們只需要知道我們的當前狀態，以便預測下一個狀態(我們不需要任何關于前一個狀態的信息)。

要使用HMMs進行預測，我們只需要計算隱藏狀態的聯合概率，然后選擇產生最高概率(最有可能發生)的序列。

為了計算聯合概率，我們需要以下三種信息:

初始狀態：任意一個隱藏狀態下開始序列的初始概率。轉移概率：從一個隱藏狀態轉移到另一個隱藏狀態的概率。發射概率：從隱藏狀態移動到觀測狀態的概率舉個簡單的例子，假設我們正試圖根據一群人的穿著來預測明天的天氣是什么(圖5)。

在這種例子中，不同類型的天氣將成為我們的隱藏狀態。晴天，刮風和下雨)和穿的衣服類型將是我們可以觀察到的狀態(如,t恤，長褲和夾克)。初始狀態是這個序列的起點。轉換概率，表示的是從一種天氣轉換到另一種天氣的可能性。最后，發射概率是根據前一天的天氣，某人穿某件衣服的概率。

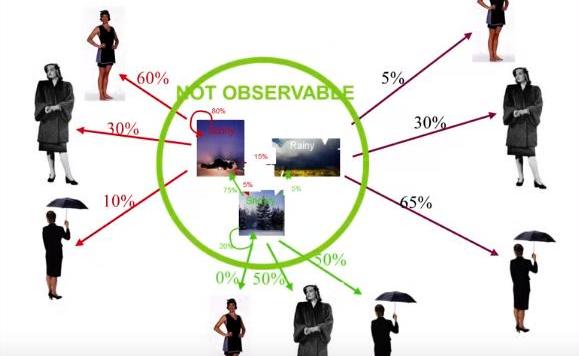
圖5:隱馬爾可夫模型示例

使用隱馬爾可夫模型的一個主要問題是，隨著狀態數的增加，概率和可能狀態的數量呈指數增長。為了解決這個問題，可以使用維特比算法。

如果您對使用HMMs和生物學中的Viterbi算法的實際代碼示例感興趣，可以在我的Github代碼庫中找到它。

從機器學習的角度來看，觀察值組成了我們的訓練數據，隱藏狀態的數量組成了我們要調優的超參數。

機器學習中HMMs最常見的應用之一是agent-based情景，如強化學習(圖6)。

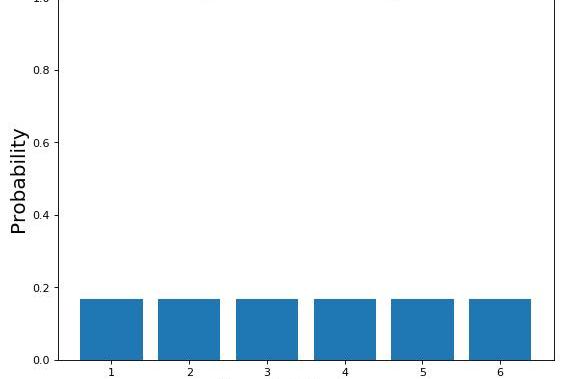
圖7:擲骰子公平的概率分布

無論如何，你玩得越多，你就越可以看到到骰子總是落在相同的面上。此時，您開始考慮骰子可能是不公平的，因此您改變了關于概率分布的最初信念(圖8)。

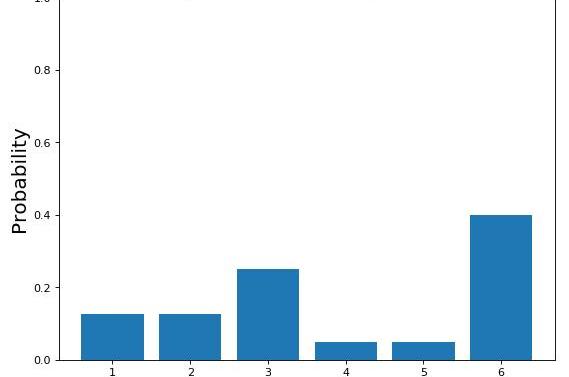
圖8:不公平骰子的概率分布

這個過程被稱為貝葉斯推理。

貝葉斯推理是我們在獲得新證據的基礎上更新自己對世界的認知的過程。

我們從一個先前的信念開始，一旦我們用全新的信息更新它，我們就構建了一個后驗信念。這種推理同樣適用于離散分布和連續分布。

因此，高斯過程允許我們描述概率分布，一旦我們收集到新的訓練數據，我們就可以使用貝葉斯法則(圖9)更新分布。

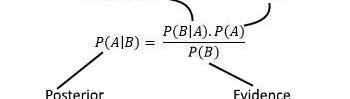
圖9:貝葉斯法則

自回歸移動平均過程

自回歸移動平均(ARMA)過程是一類非常重要的分析時間序列的隨機過程。ARMA模型的特點是它們的自協方差函數只依賴于有限數量的未知參數(對于高斯過程是不可能的)。

縮略詞ARMA可以分為兩個主要部分:

自回歸=模型利用了預先定義的滯后觀測值與當前滯后觀測值之間的聯系。移動平均=模型利用了殘差與觀測值之間的關系。ARMA模型利用兩個主要參數(p,q)，分別為：

p=滯后觀測次數。q=移動平均窗口的大小。ARMA過程假設一個時間序列在一個常數均值附近均勻波動。如果我們試圖分析一個不遵循這種模式的時間序列，那么這個序列將需要被差分，直到分割后的序列具有平穩性。

這可以通過使用一個ARIMA模型來實現，如果你有興趣了解更多，我寫了一篇關于使用ARIMA進行股票市場分析的文章。

謝謝閱讀！

參考文獻

MCEscher,“SmallerandSmaller”—1956.訪問:https://www.etsy.com/listing/288848445/m-c-escher-print-escher-art-smaller-and

機器學習中大數定律的簡要介紹。MachineLearningMastery,JasonBrownlee.訪問:https://machinelearningmastery.com/a-gentle-introduction-to-the-law-of-large-numbers-in-machine-learning/

正態分布，二項分布，泊松分布,MakeMeAnalyst.訪問:http://makemeanalyst.com/wp-content/uploads/2017/05/Poisson-Distribution-Formula.png

通用維基百科.Accessedat:https://commons.wikimedia.org/wiki/File:Random_walk_25000.gif

數軸是什么?MathematicsMonste.訪問:https://www.mathematics-monster.com/lessons/number_line.html

機器學習算法:SD(σ)-貝葉斯算法.SagiShaier,Medium.訪問:https://towardsdatascience.com/ml-algorithms-one-sd-%CF%83-bayesian-algorithms-b59785da792a

DeepMind的人工智能正在自學跑酷，結果非常令人驚訝。TheVerge,JamesVincent.訪問:https://www.theverge.com/tldr/2017/7/10/15946542/deepmind-parkour-agent-reinforcement-learning

為數據科學專業人員寫的強大的貝葉斯定理介紹。KHYATIMAHENDRU,AnalyticsVidhya.Accessedat:https://www.analyticsvidhya.com/blog/2019/06/introduction-powerful-bayes-theorem-data-science/

viahttps://towardsdatascience.com/stochastic-processes-analysis-f0a116999e4

今日資源推薦：AI入門、大數據、機器學習免費教程

35本世界頂級原本教程限時開放，這類書單由知名數據科學網站KDnuggets的副主編，同時也是資深的數據科學家、深度學習技術愛好者的MatthewMayo推薦，他在機器學習和數據科學領域具有豐富的科研和從業經驗。

點擊鏈接即可獲取：https://ai.yanxishe.com/page/resourceDetail/417

雷鋒網雷鋒網雷鋒網

Tags：ARMARMAARIARM幣是什么幣ARMA幣ARMA價格ARI價格ARI幣

火幣APP