凝聚態物理學的新篇章——超越朗道范式的拓撲量子物態_Teller:BEC

在凝聚態物理學發展歷程中，朗道—金茲堡相變理論奠定了人們對物質形態和有序相及其相變的認識基礎，在結合了威爾遜重正化群理論后，形成了朗道—金茲堡—威爾遜范式，并成為整個現代物理學宏偉大廈的重要基石。然而，在復雜電子多體系統的實驗研究中，以量子霍爾效應、分數量子霍爾效應和銅氧化物高溫超導體的實驗發現為代表，涌現了眾多超越朗道—金茲堡—威爾遜范式的新奇量子物態，掀開了凝聚態物理學的新篇章。文章從量子霍爾效應出發，介紹了二維電子體系中的幾種典型拓撲量子物態。之后，重點介紹二維強關聯電子多體系統中的內稟拓撲有序態。圍繞Kitaev提出的二維ToricCode量子自旋模型，詳細論證了該模型的基態為具有Z2內稟拓撲序的量子自旋液體，討論了其基態的拓撲簡并、低能任意子激發，以及相關的拓撲量子相變。同時，簡要介紹了內稟拓撲有序態的最新研究進展和可能的未來發展方向。

撰文|張廣銘、朱國毅

來源|本文選自《物理》2021年第9期

01

朗道相變范式

楊振寧先生認為“量子化、對稱性與相位因子是20世紀物理學發展的三個主旋律”。菲利普·安德森在20世紀70年代初就指出，多者異也(Moreisdifferent)。當大量粒子相互耦合構成一個多體系統，在低能下它將演生出與原始構成粒子所不同的集體激發準粒子，此為演生現象。比如原子構成晶體，其低能集體激發的準粒子為傳播振動與熱的聲子。然而一旦將晶體拆散分離成原子，聲子又不復存焉，所以聲子就是一種最為常見而典型的演生準粒子。演生聲子這種現象背后的根本原因是：晶體自發破缺了晶體的連續平移對稱性，隨之催生了無質量的集體激發，這種模式是對有序基態的擾動，反映了一種試圖恢復其原始對稱性的傾向。事實上，人們在大自然中所觀察到的形形色色的物質形態大多是由于其多體系統的自發對稱破缺，從而建立起長程有序的物相。

所謂“物相”，指的是一個多體系統表現出的集體宏觀性質，它不會隨著微觀參數的微小變動而改變。比如，鐵磁體在一定的溫度區間內都可以表現出磁性行為，所以叫鐵磁相。因此廣義而言，物相的定義依賴于某種絕熱原理，隨著微觀參數的變化，只要宏觀物理量的各階導數都連續，沒有碰見奇異性，則可判別為同一個物相，并具有定性一致的行為。微觀上說，物相的穩定性反映了一種集體秩序。比如，鐵磁體中不同原子磁矩由于相互作用傾向于集體同向排列而降低能量，但是熱運動又傾向于摧毀這種秩序而形成無序，所以便有了競爭。溫度的變化會干預其競爭，比如在高溫下熱運動導致無序取得勝利，而在低溫下相互作用使能量降低則戰勝了熱運動，于是在兩者之間便有了相變。

當溫度被持續調節到一定程度，達到臨界閾值，量變將引起質變，宏觀物理量將發生非解析的奇異行為，標志著相變。最早人們在實踐經驗中發現的是諸如氣液轉變這樣的伴隨有潛熱等現象的相變，其數學上對應于自由能函數的一階導數不連續性，被稱為一級相變。神奇的是，人們后來發現了氣液在更高溫度和壓強下會變得不可區分，期間經歷一個臨界點，在臨界點上自由能函數的二階導數不連續性，所以被稱為連續相變。宏觀上對相變臨界點的唯象理解最早由朗道—金茲堡(Landau—Ginzburg)的對稱破缺理論建立起來：相變的發生是由于自由能隨參數的變化導致了某種自發對稱破缺。比如低溫下原子液體進入超流相，或者金屬進入超導相是由于自發破缺了與粒子數守恒相關U(1)規范對稱性，從而建立起了宏觀的量子相干現象。因此，在朗道—金茲堡的理論中，物相由對稱性刻畫，而相變由對稱性自發破缺導致(圖1)。然而微觀上，在參數變動的纖毫之末，一個宏觀物理系統中的1023多的粒子是如何相互關聯而集體發生改變的呢？此外，更為驚人的是，大自然紛繁復雜的物質體系，其相變卻呈現出極其簡單的普適行為。后來人們發現這是因為在相變臨界點附近微觀粒子的關聯長度發散，從而系統的宏觀性質不依賴于其微觀細節，只取決于系統序參量維數和空間維數這樣的宏觀基本量。

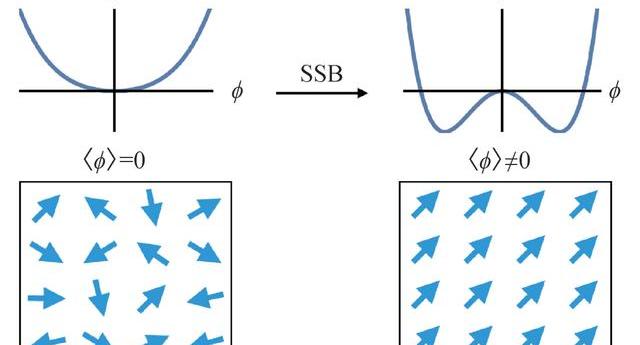
圖1朗道自發對稱破缺相變理論的示意圖。左側是無序相，其自由能F隨著序參量的函數關系如上圖所示，自由能極小對應=0。典型的例子是鐵磁耦合的原子磁矩在高溫下由熱漲落導致雜亂無序。右側是有序相，有限序參量才能使得自由能最低，因而基態會發生自發對稱破缺，即spontaneoussymmetrybreaking(SSB)，磁性系統在低溫下原子磁矩同向排列

此外，在接近絕對零度時，當改變多粒子系統的某一參數，如粒子間的耦合強度、壓力或外加磁場強度，可以將系統從一種無序的狀態連續變化到一種有序的狀態。由于在臨界點附近存在強烈的量子漲落，這類相變與僅由溫度所引起的熱力學相變完全不同，被稱為量子相變，相變的臨界點在絕對零度。量子漲落是導致量子相變的根本原因，其來源是量子系統中物理量的非對易性。一個典型的例子是，受橫向磁場作用的一維伊辛(Ising)模型，隨著磁場的增強，該模型會出現從鐵磁相到順磁相的量子相變。這類相變，盡管是發生在絕對零度，但依然可以納入朗道對稱破缺的二級相變理論框架之中。

對稱破缺相變的微觀定量描述由威爾遜(Wilson)所提出的重正化群理論來奠基，其基本思想是考慮熱力學(量子)漲落，在標度變換下，通過逐級計算短程高能的物理效應來修正微觀粒子間的耦合系數，最終得到長波低能極限下的有效物理作用量。由此，描述相與相變的朗道—金茲堡—威爾遜(Landau—Ginzburg—Wilson，LGW)范式猶如一座大廈落成，而對稱性也成為凝聚態物理領域研究物相與集體激發行為的主旋律。

此外，二維經典物理體系會出現一種特殊的熱力學相變，即Kosterlitz—Thouless(KT)相變。根據Mermin—Wagner定理，我們知道在具有連續對稱性的二維體系中，熱漲落會抵抗連續對稱性的自發破缺，摧毀有限溫度下的長程序，從而導致有限溫度下不可能發生有序相變。然而，在1973年Kosterlitz與Thouless發現，由于經典渦旋拓撲激發的參與，有限溫度下可以發生不破缺連續對稱性的連續相變。在高溫無序相，關聯長度有限，關聯函數隨空間距離指數衰減，而跨越臨界點進入低溫相之后，關聯函數呈現冪律衰減，而且具有普適的標度行為，介于長程序與無序之間，叫準長程有序，其背后的物理圖像是系統中的渦旋拓撲激發形成束縛態。作為超越LGW范式的最早例子，這里的渦旋拓撲激發因為相對直觀而且最早進入人們的視野，所以早期的凝聚態物理學家還曾將Kosterlitz—Thouless相變溫度以下的這個無能隙準長程序稱作“拓撲序”，此概念與后來人們所關注的有能隙相中的拓撲序概念不可同日而語。

礦企Core Scientific 8月份產出1334枚比特幣，售出1125枚比特幣:9月7日消息，比特幣礦企Core Scientific發布8月份生產和運營更新，Core Scientific的自挖礦業務在8月份生產了1334枚比特幣。自挖比特幣生產受益于本月約17,000臺新服務器的部署。多個數據中心的削減活動增加限制了生產進展。

該公司在本月將其自挖礦服務器機群擴展至127,716臺，將哈希率提高至12.69 EH/s。公司預計在2022年底前額外部署約43,000臺自挖ASIC服務器。截至8月31日，Core Scientific還為超過97,000臺客戶擁有的ASIC服務器提供數據中心托管服務、技術和運營支持。

在8月份，該公司以23014美元的均價出售了1125枚比特幣，總收益約為2590萬美元。截至8月31日，公司持有1409枚比特幣和約4,720萬美元現金。[2022/9/7 13:13:16]

自20世紀80年代開始，人們陸續從實驗中發現超越LGW范式的量子多體物質形態。這些物質形態都不具備對稱破缺導致的長程序，但是它們之間的轉變又不可避免要經歷奇異性，亦即發生相變。根據絕熱原理，它們應當屬于不同的物相。因此，LGW范式預言“沙漠”之中尚有形態各異的“綠洲”。這類超越LGW范式的物相，盡管沒有對稱性的區分，卻有著拓撲性質上的差異。所謂對稱性，原來是指系統在某種微觀操作下的不變性，比如微觀粒子的集體平移、旋轉；而所謂拓撲性質，是指系統具有一些離散的整數化的宏觀物理量，且這些物理量不隨著輕微擾動而改變。比如，常見的一個紐結不隨著繩子形變而解開，一個渦旋不隨著擾動而消逝，一個甜甜圈一般的圓環面不隨著扭捏而化作球面。在量子多體系統中的拓撲往往體現在某種集體激發準粒子波函數的相位因子上，比如在閉合軌跡下積累了不依賴于具體動力學的量子化Berry相位。因此，量子多體系統中演生出來的物相及其相變，繼續體現著楊振寧先生曾經所概括的三個主旋律。

02

超越朗道范式的拓撲量子物態

以二維量子霍爾效應為范例，我們簡要回顧拓撲物相的發展，試圖勾勒出弱相互作用系統中拓撲電子態的基本物理。在固體材料中，弱相互作用的電子由于量子效應而形成分立的能帶結構，從而可以形成絕緣相。在絕緣相中，電子激發態需要克服有限能量，因而在低能下沒有電子激發，似乎與真空無異。然而，自從20世紀80年代發現量子霍爾效應以來，人們發現在絕緣體中有一大類特殊的絕緣體，盡管其塊體內無低能的電子激發，但是在其邊緣上卻有不需要克服能量的無能隙激發態，并且還具有強的魯棒性，其背后的根源正是拓撲相位因子。

2.1量子霍爾效應

在磁場中，二維電子氣會受到洛倫茲力而圍繞磁通發生回旋運動，在能譜上形成朗道能級，其能級間距正比于回旋頻率，取決于磁場大小和電子有效質量。每個能級具有與體系尺寸相匹配的巨大簡并度，因為在實空間上每個量子磁通就對應于一個電子軌道。由于泡利不相容原理，當電子填滿整數個能級的時候，再增加一個電子需要克服系統能隙，所以該體系為“不可壓縮”絕緣態。盡管體內激發具有能隙，但在實驗上觀測到量子化的橫向電導表明其系統邊緣存在穩健的單向流動的無能隙電子態模式，這就是量子霍爾效應。橫向電導的量子化暗示了其內在的拓撲性。在1982年，Thouless，Kohmoto，Nightingale與denNijs四人首次提出了TKNN公式來刻畫量子霍爾態的拓撲本質，并且將其體塊和邊緣的橫向電導聯系了起來。TKNN公式本質上就是從集體激發的電子波函數中提取出Berry相位。

要理解Berry相位通量的量子化，一個最簡單而又具有代表性的例子就是考慮一個連續動量空間中的狄拉克(Dirac)旋量波函數，粒子受到磁單極子的作用：

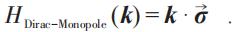
其對應的基態本征波函數為

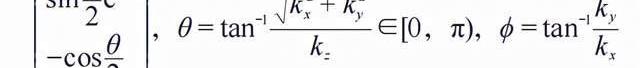
其中θ，為球面角參數。然后，我們可以求得Berry聯絡：

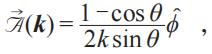
以及在不同緯度圓軌跡上的Berry相位：

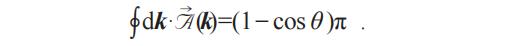
當θ=0，也就是環繞北極點的無窮小軌跡其獲得相位為0；當θ=π/2，其獲得π相位；而當θ=π，將獲得2π相位。也就是說，磁單極子具有2π的量子化的Berry通量。確實，狄拉克磁單極子攜帶著一根具有2πBerry通量的狄拉克弦。在我們這個例子中，該弦從奇點向南極無窮延伸，如圖2所示。此外，狄拉克磁單極子Berry通量的量子化與二維空間中的Berry通量的量子化密切相關。只要我們取一個映射：

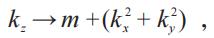
其中m代表狄拉克費米子的靜質量。如此定義了從二維空間到三維空間的一個曲面映射，直觀上相當于將二維動量平面嵌入到三維空間中，或者說把三維中的一個曲面攤開延展到二維平面(圖2)。簡單分析看到，當m<0，二維動量平面相當于完全包裹了一個磁單極子，從而獲得2π的Berry通量。反之，m>0則對應于0通量。通過這個簡單而又具有代表性的例子，我們可以窺見，二維封閉流形中的Berry通量量子化本質上是因為三維空間中磁單極子的量子化，對應于二維空間中的一個拓撲結構，稱為斯格明子(skyrmion)。

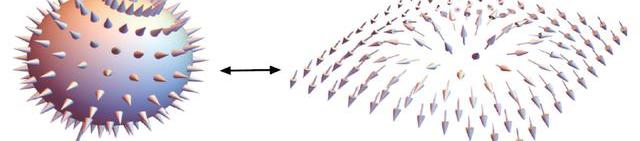
圖2將包裹著一個狄拉克磁單極子的球面延展到一個平直二維平面，即斯格明子(skyrmion)

由于拓撲量子數具有魯棒性，只要系統的能隙不被關閉，則不能發生改變。人們將這樣得到的量子數稱為拓撲陳數(Chernnumber)，因為其背后的深刻數學描述是由陳省身先生研究創建的纖維叢理論。由于這樣的絕緣體體內具有非零的拓撲陳數，而體外的真空等價于拓撲陳數為零，則其邊緣作為兩者的過渡區域必然要發生某種特殊的低能物理特征來彌補拓撲數之差，這便是單向傳輸(手征性)的無能隙邊緣量子電子態模式。也就是說，邊緣模式是由于體內與體外的拓撲差別，因而必然具有魯棒性，不受邊緣形狀、雜質散射所影響，而且邊緣模式的數目也會由體內的拓撲數完全決定，所以完美解釋了實驗觀測到的量子化橫向電導。

安全團隊：BNB Chain上GXY代幣發生Rug Pull:金色財經報道，據CertiK監測，BNB Chain上GXY代幣發生Rug Pull，不要與其他Galaxy Coin代幣混淆。0xBf43開頭地址昨天開始移除流動性，并繼續出售代幣。約79000美元已轉移到外部賬戶（EOA）0x1064。[2022/8/30 12:57:21]

2.2量子反常霍爾效應

自整數量子霍爾效應從理論上被解釋之后，人們很快設想在電子多體系統中，即使在沒有外加磁場的情況下也可以發生量子霍爾效應，因而被稱為量子反常霍爾效應。1988年，Haldane最先提出了一個理想模型，可以實現量子反常霍爾效應。在一個描述石墨烯低能物理的六角晶格無自旋電子緊束縛模型中，電子只能在近鄰格點之間躍遷。由于六角晶格的元胞包含兩個格點軌道電子，因此可以在布里淵區(Brillouinzone，BZ)中得到兩條能帶，而兩條能帶在BZ角點K與-K上發生點接觸，形成局部線性色散的狄拉克錐。也就是說，盡管原始構成粒子為非相對論性的緊束縛電子，然而在低能下，該系統中的電子表現為一對具有線性能動量關系的無質量狄拉克費米子(圖3)。

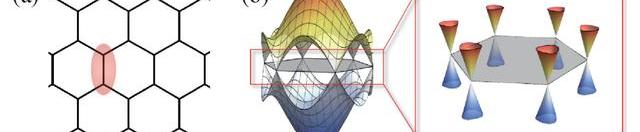
圖3(a)六角晶格；(b)六角晶格最近鄰躍遷模型在動量空間中的能帶色散關系及其低能狄拉克錐。黑色六邊形標記BZ，平均每個BZ分得一對狄拉克錐

Haldane在這樣的模型中引入一個帶相位的次近鄰電子躍遷項，使得低能狄拉克費米子獲得質量。尤為重要的是，他施加的躍遷相位正好使得兩個狄拉克費米子獲得相反符號的質量，一正一負。狄拉克費米子獲得質量則意味著在能帶上打開能隙，可以通過計算拓撲陳數發現，其中一個能帶具有+1的陳數而另一個能帶的陳數為-1，從而完全填充其中一個能帶便可實現量子反常霍爾效應。直觀上看，一個帶質量的狄拉克費米子可以攜帶±π的Berry相位通量，而兩個組合起來則可以為2π或0兩種可能。在Haldane模型里，當取相同的質量則得到0通量，而相反質量則得到2π通量。值得注意的是，這樣的模型盡管沒有外加磁場，但是依然不可避免地破壞了時間反演對稱性。事實上，這是因為電子波函數的相位在時間反演下反號，從而拓撲陳數也繼承了這樣的行為，非零陳數必然意味著時間反演對稱性的破壞。

2.3量子自旋霍爾效應

隨后人們發現了一個反例，或者說是對原來的拓撲陳數的推廣。2004年，C.Kane與E.Mele在Haldane模型的基礎上，進一步考慮到自旋軌道耦合效應提出了一個新的理想模型。由于存在電子自旋自由度，他們的模型在低能下本質上相當于將兩個Haldane模型，分別對應自旋上和自旋下，以相反的方式來破缺時間反演對稱性，從而在整體上維護系統時間反演對稱性。然而，只要保證兩個自旋自由度不發生耦合散射，則其各自的拓撲數仍然可以良好定義并且滿足守恒定律，即自旋自由度為好量子數。更一般而言，該體系只需要時間反演對稱性保護，狹義的“拓撲絕緣體”指的就是這樣的在時間反演對稱性保護下具有非平庸Z2拓撲數的絕緣體。拓撲性質導致在體系邊緣上，產生分別對應兩種自旋自由度而反向運動的無能隙電子流，從而形成拓撲保護的手征自旋流。換個角度看，其邊緣上相當于產生了無質量的自旋軌道鎖定的螺旋電子運動模式，這樣的拓撲相被人們稱為量子自旋霍爾態。后來，與之等價的拓撲相也被張守晟等人預言會在HgTe—CdTe量子阱中實現。自此，拓撲絕緣體受到許多人的關注，并開辟了一個全新的領域。

不難發現，由于量子多體系統中還有許多其他的自由度，類似于量子自旋霍爾效應的推廣還可以有許多，比如量子能谷霍爾態。除此之外，拓撲絕緣體不限于二維，在三維體系中人們也提出了類似的Z2拓撲數的概念。借助于量子自旋霍爾效應的平臺，通過摻入磁性雜質來主動破壞時間反演對稱性，薛其坤團隊首次觀測到了量子反常霍爾效應，從而在實驗上首次驗證了量子反常霍爾效應。這一大類的拓撲材料由于具有拓撲保護的邊緣傳輸模式，包括電荷、自旋輸運模式，乃至能谷輸運模式，因而在低功耗自旋、能谷電子學器件應用上具有廣闊前景。

2.4二維拓撲超導態

最簡單的二維拓撲超導是具有軌道角動量l=±1的p±ip無自旋費米子超導，以及l=±2的d±id自旋單態配對的超導。根據泡利不相容原理，無自旋費米子的配對波函數其軌道自由度必然要具有反對稱性，在有單軸旋轉對稱性的前提下意味著奇數的角動量，則最簡單的例子便是px+ipy。在連續極限下，低能有效哈密頓量可以寫為

轉換到動量空間中，上式成為

其中，我們將電子和空穴組成二分量的旋量，而ρ則是作用在該旋量空間中的三個泡利算符矩陣。因此，有效哈密頓量表示為贗磁場與贗自旋的作用，該磁場在動量空間中的分量為

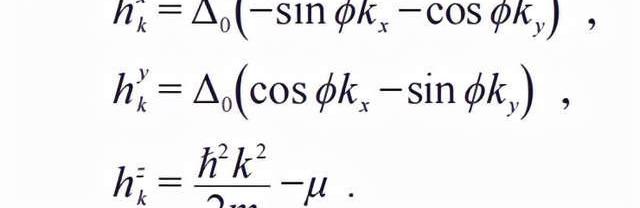
其形式等價于我們先前所討論的狄拉克二分量旋量費米子哈密頓量式，這里的拓撲直接體現在背后的贗磁單極子的量子化。只有當化學勢μ=0的時候，準粒子激發譜在k=0處關閉能隙，除此之外，系統具有有限大的能隙。因此，μ=0是一個臨界點，分開了兩個有能隙超導相。這兩個超導相具有完全一樣的對稱性，但是它們有著不同的拓撲陳數：C=1，μ>0，而C=0，μ<0。也就是說，μ>0時，化學勢從能帶中切割出費米面，此時的超導具有非平庸的拓撲性質，對應弱配對的巴丁—庫珀—施里弗(Bardeen—Cooper—Schrieffer，BCS)極限；而μ<0時，系統不具有費米面，此時的超導是平庸的，對應于強配對的玻色—愛因斯坦凝聚(Bose—Einstein—Condensation，BEC)極限。

與常規s波配對超導態不同，p波超導的弱配對BCS極限與強配對BEC極限并不絕熱相連，其拓撲不等價性導致必然需要經歷一個拓撲相變。考慮μ>0的一個足夠大且具有開放邊界的系統，由于從系統內部到外面的真空經歷了拓撲陳數從C=1到C=0的變化，在系統的邊緣上必然要關閉能隙。在開放邊界條件下，通過求解Bogoliubov—deGennes方程得出，在邊緣上將出現手征性、單向性準粒子傳導，即破壞了時間反演與宇稱的馬約拉納(Majorana)費米準粒子模式。

加密貨幣支付應用Strike推出新Visa卡，將提供消費獎勵:金色財經報道，基于閃電網絡的加密貨幣支付應用Strike宣布推出一張新的Visa卡。該公司在其推特上宣布了這一消息，并表示其用戶現在可以“把Strike帶到任何地方，并在日常消費中獲得獎勵”。推廣工作將從等待名單開始。在推文中，Strike稱，用戶將能夠使用新卡直接存款，以比特幣支付，購買比特幣，發送和接收資金，使用Apple Pay和Google Pay消費，并在消費時獲得獎勵。（The Block）[2022/8/12 12:20:47]

更進一步，我們可以求解出，當超導體塊中出現了超導渦旋的時候，將會俘獲一個嚴格零能量的孤立馬約拉納費米子。這可以如下簡單理解：將超導渦旋近似處理成超導體上一個挖空的圓對稱的區域，則圍繞其邊緣會出現線性色散的手征馬約拉納費米子模式，而由于磁通渦旋的存在抵消掉了p+ip超導自身攜帶的2π相位環繞。所以，該手征馬約拉納費米子模式波函數滿足周期邊界條件，從而其軌道角動量整數量子化，其中角動量為0的模式則為嚴格零能量的馬約拉納費米子。事實上，其零能量受到拓撲保護，在擾動下該結論不變。磁通渦旋與俘獲的孤立零能量馬約拉納費米子的復合體被稱為馬約拉納零能模式。與單純的費米子不同，馬約拉納零能模具有非阿貝爾的統計，即兩個馬約拉納零能模相互纏繞一周彼此都會獲得π相位。如何在實際物理體系中實現p+ip拓撲超導？2008年，傅亮和C.Kane提出在拓撲絕緣體表面態上耦合常規超導體可以實現p+ip拓撲超導，該方案吸引了許多實驗學者的關注。其方案的核心是，借助三維拓撲絕緣體表面態上的狄拉克螺旋電子態的強自旋軌道耦合，有效地“凍結”電子自旋自由度，從而演生出p+ip的低能有效配對拓撲超導態。

此外，我們簡要介紹下一個d+id拓撲超導。其超導配對波函數的軌道角動量l=2，具有偶宇稱，因而出現在自旋單態配對中。d+id的配對波函數圍繞費米面會發生4π的相位環繞，因此得到拓撲陳數C=2，在邊緣上會導致兩支手征馬約拉納模式，等價于一支狄拉克費米子模式。此外，考慮到自旋單態配對不破壞SU(2)對稱性，所以Bogoliubov準粒子激發攜帶自旋簡并，從而其邊緣模式即為一支攜帶自旋的狄拉克費米子模式。因此，盡管d+id超導也具有非平庸的拓撲，但是其邊緣乃至渦旋中心都不具備孤立的馬約拉納模式，從而屬于阿貝爾統計類型。有研究者認為在1/4填充附近的石墨烯或者在三角晶格的哈伯德模型中可以實現d+id拓撲超導。

2.5相應的拓撲相變

按照絕熱原理，有序相的劃分依賴于相變，因而有序相與相變猶如一枚硬幣的兩面不可分割。在傳統的LGW范式中，有序相由序參量來刻畫，相變則對應于序參量獲得一個非零真空期望值，相變理論基本決定于宏觀的序參量和空間維數。因而物質的有序相及其相變有一一對應關系，知道了兩個相，從對稱性和空間維度的信息便基本確定了其間的相變臨界理論，這就是凝聚態中的普適類的概念。與傳統LGW相變不同，拓撲相變并不涉及對稱性破缺，大多由拓撲數來刻畫，因而其拓撲陳數的改變則標志著拓撲相變，類比于LGW范式下對稱性的改變所描述的相變。在此類拓撲臨界點上，往往具有無質量狄拉克色散的費米子激發，其數目取決于兩邊拓撲相的拓撲數之差，狄拉克費米子質量出現反號，則對應拓撲相變的相變點。比如平庸絕緣態到量子自旋霍爾態的相變，在低能下對應于一個二維螺旋狄拉克費米子從正質量變為負質量。

03

超越朗道范式的內稟拓撲有序物態

諸如量子霍爾態、量子反常霍爾態和拓撲超導態這樣的量子多體糾纏態，由于無法絕熱地演變成單粒子直積態，它們的拓撲性質體現在邊緣上或者缺陷上的無能隙穩健激發模式，而體內并沒有任何不同于平庸相的物理效應。然而，在粒子與粒子的強相互作用下，量子多體系統還可以演生出更加豐富的內稟拓撲有序物態，其拓撲本質則體現在體內可以出現新奇準粒子激發，它們滿足的統計性質既非玻色亦非費米統計。

3.1任意子統計

通常在三維空間中，點狀粒子與粒子之間的任何纏繞軌跡均可以絕熱連續收縮回到原點，從而粒子與粒子之間的纏繞必然只能產生0或者2π的統計相位。由于兩次粒子交換操作等價于粒子之間的纏繞，所以粒子之間的交換只可能導致其波函數相位改變0或者π，分別對應于玻色子與費米子。然而在二維空間中，粒子之間的纏繞軌跡無法絕熱地收縮回到原點，從而原則上可以獲得更為一般的Berry相位(圖4)。在二維空間中，原則上可以出現超越玻色子與費米子的其他分數化統計相位的粒子，F.Wilczek最早提出，并稱之為“任意子”(anyon)。任意子之中又分為阿貝爾任意子與非阿貝爾任意子，前者的相互纏繞只導致波函數整體相位的改變，而后者對應于矩陣形式的相位因子，所以相互纏繞導致波函數被完全改變。任意子在2+1維時空中相互纏繞的世界線等價于數學上的辮子群。

圖4(a)在三維空間中，點粒子之間的纏繞軌跡可以沿著球面絕熱收縮回一個點，因而產生的相位只能為0(玻色)或者π(費米)；(b)二維空間中，點粒子之間的纏繞軌跡由于被禁錮在二維平面內而無法絕熱地收縮回一個點，因而原則上可以產生任意的Berry相位，包括非阿貝爾類型

這些超越玻色與費米統計的任意子便演生于強相互作用的內稟拓撲有序態之中。最為著名的例子便是實驗中所觀測到的分數量子霍爾態，盡管其微觀基本自由度都只是電子，但是其強相互作用的結果導致在低能長波極限下所觀測到的準粒子具有分數電荷并滿足統計，比如最早觀測到的電子比上磁通的填充數ν=1/3的Laughlin霍爾態，其準粒子激發即具有1/3電荷的統計性質，堪稱凝聚態中的夸克；而知名的ν=5/2填充的Moore—Read態則具有非阿貝爾的伊辛任意子激發。由于具有有限能隙，分數量子霍爾效應在低能長波極限下的規范漲落可由Chern—Simons拓撲規范理論所描述，所以對應的量子態具有拓撲有序性質。

此處的拓撲，本質上是因為系統的低能有效作用量不依賴于時空度規，即在時空坐標變換下作用量保持不變，而表征上體現在這些具有非平庸統計相位的任意子類似于拓撲激發，具有強魯棒性。同時任意子從產生到湮滅的運動軌跡可以將一個多體基態轉變為另一個基態，從而導致依賴于實空間的流形拓撲的基態簡并度。任意子的信息完全蘊含在系統基態空間中，可以通過對實空間流形作模變換而提取出任意子的統計相位。比如，將實空間上的一個圓環面作90°旋轉的變換，在基態空間中的表示矩陣描述了不同任意子之間相互纏繞的統計相位；而將圓環面剪切開，將其中一個開口自轉90°再重新接上這樣的變換矩陣則攜帶了同種任意子之間纏繞的統計相位。有了任意子之間的統計相位信息，便可以通過Verlinde公式計算出任意子的基本融合規則，實現拓撲有序態的完整描述。

STEPN與日本通訊巨頭LINE加密子公司達成合作:8月8日消息，STEPN運營商Find Satoshi Lab Limited與日本通訊巨頭LINE旗下加密貨幣和區塊鏈子公司LINE Xenesis簽署諒解備忘錄，將使用LINE的專有區塊鏈“LINE Blockchain”在日本提供本地化的“MoveandEarn”服務。[2022/8/9 12:11:47]

3.2量子自旋液體

另一個能演生任意子的內稟拓撲物態則是量子自旋液體家族。量子自旋液體的研究可以追溯到阻挫量子磁學以及銅氧化合物高溫超導體。30年前，安德森提出共振價鍵態(ResonantValenceBonds，RVB)的擬設，用來作為阻挫量子磁性基態甚至作為高溫超導的母體態。在具有電子半滿填充的晶格體系中，由于強庫侖相互作用，電子電荷自由度被凍結，只留下自旋自由度，形成強關聯莫特絕緣相。在經典理論中，低溫下自旋熱運動被凍結，自旋傾向于破缺旋轉對稱性形成某種量子有序態，比如鐵磁態和反鐵磁態，或者保留自旋旋轉對稱性而破缺晶格對稱性的價鍵固態：電子兩兩配對成為價鍵單態。然而，電子磁矩在反鐵磁的超交換作用下，強烈的自旋量子漲落會摧毀任何的有序而恢復高對稱性。當存在晶格幾何阻挫時，量子漲落的效應尤甚。由于沒有破缺任何的自旋旋轉對稱性和晶格對稱性，人們將其喻為“量子自旋液體”。量子自旋液體最有代表性的就是由安德森提出的作為許多不同的價鍵固態的等權量子疊加的RVB液體態。在該量子態中，電子的自旋和電荷自由度分離而出現分數準粒子激發，演生出的規范場傳遞粒子間相互作用。在RVB擬設下，自旋子(spinon)已然發生配對，而在進行空穴摻雜時，U(1)規范對稱性上升為全局對稱性，空穴子(holon)作為玻色子可以發生玻色凝聚而自發破缺全局的U(1)對稱性，這時系統便進入到超導相，這便是高溫超導的RVB圖像。

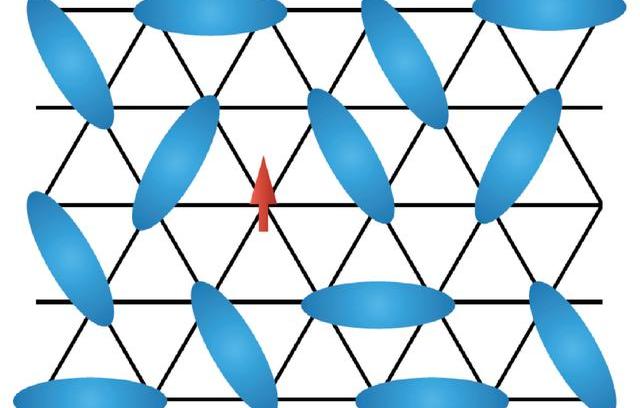
圖5示意最近鄰短程共振價鍵態(RVB)中的其中一個價鍵態構型。藍色橢球標記一個由兩個格點上的自旋所形成的自旋單態，紅色標記一個孤立自旋子(spinon)拓撲激發，其滿足費米統計但不攜帶電荷

然而，基于高溫超導體系的RVB是由長程的自旋單態組成，其自旋子無能隙而具有費米面，研究起來非常復雜。為此，Rokhsar與Kivelson提出了量子二聚態模型，考慮更原始的短程RVB態中的拓撲激發，用簡化的二聚化構型來刻畫短程RVB的極限，即退禁閉的自旋子以及演生渦旋規范場，如圖5所示。而文小剛則從隸玻色子(slaveboson)分解與演生規范場的角度提出了該體系中的Z2拓撲序的概念。隨后，Moessner與Sondhi從數值計算上驗證了該系統所具有的Z2拓撲序。然而，真正徹底的征服來自1997年Kitaev在arXiv上發布文章所提出的嚴格可解模型，該模型簡單且嚴格可解，展現出相應的克服能隙的任意子激發與基態拓撲簡并。

3.3Z2自旋液體態

1997年，A.Kitaev在arXiv上發布一篇名為《藉由任意子實現可容錯的量子計算》的文章，首次提出一個名叫ToricCode的自旋模型，名字取義于在圓環面上作量子編碼，文章后來正式發表于2003年。該自旋模型嚴格可解，其基態為量子自旋液體，可以完美地展示Z2內稟拓撲序。該模型十分簡約，只保留了最核心的拓撲的信息。與RVB自旋液體不同，此模型并不具有自旋旋轉不變性，從而充分展示了Z2量子自旋液體的本質不在于對稱性。出于這個模型的極簡性與嚴格可解性，以及Z2內稟拓撲序的基礎性，該模型在拓撲序研究領域中的地位堪比伊辛模型在相變研究中的地位，是許多理論和實驗研究的一個試金石。

ToricCode模型最初定義在一個周期邊界條件的正方晶格上，自旋1/2物理自由度處于格點連邊上，其哈密頓量表示為

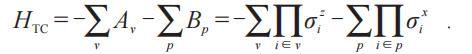
其中頂點Aj算符與元格Bp算符分別定義在頂點與元格(plaquette)上，如圖6(a)所示。四自旋相互作用項表面上十分復雜，但是每一個局域的Aj或者Bp都是守恒量，這是由于自旋1/2的泡利算符反對易，而頂點算符和元格算符之間總有偶數自旋交疊，從而抵消了負號。因此，任意的本征態都可以由所有的局域算符的本征值來完全確定，模型嚴格可解。

圖6(a)ToricCode模型中四個自旋乘積形成的相互作用項；(b)ToricCode模型的基態可以表示為所有閉弦等權相干疊加形成的弦網凝聚態

當我們將自旋朝上視作參考真空，而自旋朝下看作弦的一段，那么ToricCode模型的基態可以表示為包含所有閉弦等權重相干疊加態，如圖6(b)所示。這種閉弦凝聚態可以看成是傳統玻色子凝聚態從點粒子推廣到弦這樣的延展對象，并且閉弦在基態中可以任意漲落不耗散能量。其實，在經典伊辛統計模型中，高溫極限下自旋無序漲落，磁疇壁發生任意的熱漲落。如果把閉合疇壁當作基本自由度，該熱力學系統則為發生熱漲落的各種疇壁。這樣的伊辛統計模型與ToricCode模型的基態有著深刻的內在聯系。

實際上，ToricCode模型等價于一個描述二維空間中最簡單的離散化的電磁場理論，其低能激發包含的準粒子有：電荷e、磁通m、馬約拉納費米子f。由于不同格點的σx之間相互對易，所以m粒子相互纏繞的軌跡算符可以等價于一串m閉弦算符作用到基態波函數上，并不出現任何相位，從而m粒子之間具有玻色統計。同理，不同的e粒子相互之間纏繞也不產生相位而同樣具有玻色統計。然而，關鍵的是當一個e粒子環繞一個m粒子一周纏繞時，其運動軌跡涉及一條e弦與一條m弦的相交。由于σxσz=-σzσx，從而它們之間的交換會貢獻一個“-1”，即導致π的Berry相位，如圖7所示。也就是說，盡管各自滿足玻色子統計，但是e與m粒子相互間卻具有非平庸的統計相位π，人稱“semion統計”。如此一來，可以簡單驗證，e粒子與m粒子的復合粒子具有費米統計，記為f=em。從一個純粹的玻色自由度的微觀模型中，竟然演生出了費米子激發，這不可不謂神奇！如此，我們便確立了該體系中的三種基本低能拓撲激發準粒子e，m，f。廣義上說，它們都屬于任意子。

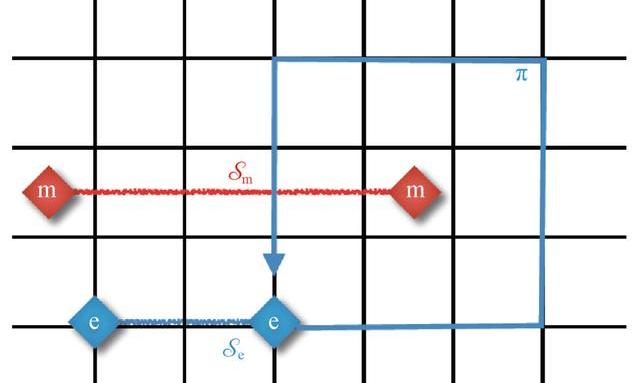
圖7弦算符激發的拓撲粒子及其統計關系。藍色粗線代表電荷e弦，紅色粗線代表磁通m弦，其各自末端為拓撲準粒子。可以驗證電荷e弦環繞磁通m弦一圈后，發生Aharonov—Bohm效應導致π相位

烏克蘭央行新的法定貨幣限制或將促進加密貨幣普及:7月24日消息，烏克蘭中央銀行(NBU)將烏克蘭貨幣格里夫納兌美元貶值25%，并對公民的格里夫納交易實行了更嚴格的限制。烏克蘭加密貨幣交易所 Kuna 的創始人 Mikhail Chobanyan 表示，最新的 NBU 限制可能會導致烏克蘭人對加密貨幣的興趣激增。（Bitcoin.news）[2022/7/24 2:34:18]

每一種任意子激發都具有拓撲穩定性，不同的任意子類型只能通過融合來轉變，比如e型任意子只能通過與f型任意子融合來得到m型任意子。一般而言，任意子的融合遵循一個簡單而基本的代數原則。ToricCode模型任意子的融合原則是

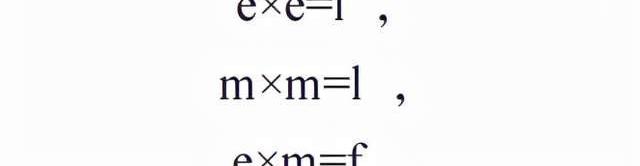
事實上這組融合規則連同任意子的統計定義了一種拓撲序。在三角晶格短程RVB自旋液體中，雖然微觀晶格不同，對稱性也不一樣，但是其中的基本拓撲激發卻遵循同樣的統計和融合規則，即費米型的自旋子圍繞著玻色型的演生規范場vison(π通量渦旋)轉一圈會產生π通量激發。所以，三角晶格上的短程RVB自旋液體與ToricCode模型同為一個普適類，稱為Z2拓撲有序。之所以稱作Z2，是因為其低能激發演生出了Z2規范場。

盡管ToricCode模型是在離散的正方晶格上通過自旋模型定義的，但是其封閉弦凝聚的基態圖像具有長波極限的特質，因而可以推廣到任意的微觀晶格。一般性而言，可以完全脫離晶格而通過定義一組連續化的弦構型來構造屬于同一個普適類的Z2內稟拓撲序。除此之外，通過定義更豐富代數結構的弦構型，還可以得到更加廣泛的弦網凝聚拓撲態。由于弦的非局域特質，這些模型都具有自帶拓撲穩定的任意子激發，即內稟拓撲序。事實上，MichaelLevin與文小剛在2005年的工作中展示，弦網凝聚圖像可以演生出所有的二維非手征的拓撲序。因而，弦網凝聚是一個強有力的物理圖像，它從某個角度簡明直觀地概括了非手征拓撲序的本質屬性。

事實上，由于基態的局域特征已經被穩定子算符鎖死，即局域上不存在開放的e弦或者m弦，所以如果將體系放在一個球面上，則只有唯一基態。盡管很難想象如何將正方晶格放置在球面上，但是閉弦凝聚卻可以置于連續空間中，所以可以放置在球面上乃至更一般的拓撲流形上。然而，對于兩個方向都為周期性邊界條件的正方晶格，相當于將閉弦凝聚體放置在一個圓環面上，這時候環繞兩個不可收縮大圓的全局閉弦數目的奇偶性將導致出現四個正交的簡并基態。由于局部漲落只能產生可收縮的局部閉弦，全局閉弦可以發生形變或者成對漲落，但是其數目的奇偶性不會改變，因而是一個穩定的全局量子數。不同的基態可以用全局弦算符來轉換，也可以用對偶的橫向全局弦算符來探測。具體而言，我們可以定義環向(x方向)和極向(y方向)不可收縮的全局e弦和m弦算符，如圖8所示，可以驗證除了相互垂直的全局e弦與全局m弦之外，其他的都相互對易。

圖8以兩個方向的m弦數目奇偶性來區分的m弦表象的四重簡并基態。其中裸的圓環面代表基態，帶紅圈的表示攜帶了全局弦算符。環向為x方向，而極向為y方向。對偶變換可以得到e弦表象下的四重簡并基態

全局的弦算符作用到一個基態上使之變成另一個基態，這從物理圖像上說其實就是產生一對任意子激發，并且使之圍繞體系大環環游，其后再發生湮滅。由于四重簡并基態之間只能通過全局的弦算符來聯系，從而局域的微擾需要通過體系尺寸大小級別的巨大微擾才能將一個基態轉換到另一個基態，導致兩個基態在微擾下能級劈裂隨著體系尺寸指數衰減。所以ToricCode模型的簡并基態受到拓撲保護，這也正是為何Kitaev提出可以使用這類模型來編碼量子信息，從而可以從物理層面上實現容錯。

此外，弦的量子數只有奇偶守恒，可模2漲落，這其實也是Z2拓撲序內在的Z2對稱性的一個體現。事實上，如果將該模型推廣到更一般的拓撲流形上面去，比如包含g個虧格的流形，可以形象地理解成具有g個洞的廣義面包圈，則按照同樣的邏輯可以導致更高的基態簡并度4g。也就是說，基態簡并度依賴于其所處在的實空間流形的拓撲，從而有所謂“拓撲序”一詞。注意到這里的拓撲是實空間的拓撲，跟前面討論到的動量空間上的渦旋和斯格明子等拓撲結構有本質不同。考慮到該體系具有有限的能隙，從而任意的局域關聯函數都是短程關聯，具有有限關聯長度，那么如此一個“短視”的體系是如何“感知”到流形整體的拓撲的呢？這背后的根本原因在于長程的量子糾纏。量子糾纏是一種量子性的關聯，并不能用普通的局域算符的關聯函數度量之。

另外，在一般微擾下，ToricCode模型其實可以對應一個具有電磁對偶的Z2規范理論，即二維空間中一個最簡單的離散版本的電磁理論。其中基本激發粒子正是電荷e、量子磁通m，以及二者復合而成的費米子f。磁通的量子化不禁讓人聯想起二維超導態。其實ToricCode模型和Z2規范理論正是描述了二維超導態的低能規范動力學行為。通常的量子電動力學中，電子具有U(1)規范對稱性，從而電荷數守恒，而其磁通則可以連續變化。在發生安德森—希格斯超導相變之后，U(1)規范對稱性下降為Z2，從而電荷數守恒下降為奇偶守恒，相當于把整數的加法運算下降為模2的加法運算。而超導磁通渦旋則被量子化為π通量，庫珀對探測到的2π通量相當于單個電子或空穴所探測到的π通量。在常規的s波超導相中，通常考慮的基本低能激發只有馬約拉納費米子。盡管沒有外磁場的注入，如果將規范漲落動力學也考慮進來，把系統自身量子漲落產生的超導渦旋看作一種內稟的磁通自由度，則還有馬約拉納費米子與內稟磁通的復合體。可以驗證，這正是玻色型的電荷e=mf粒子，見表1。如此一來，ToricCode模型和Z2規范理論并不是十分抽象神秘的理論，而是一個最簡單的對偶的電磁理論，描述著凝聚態中熟知的超導相的低能規范漲落的物理。因此，受此啟發，Sondhi等人從規范動力學的角度認為超導有序本質上都是超越朗道對稱破缺的拓撲有序態。

表1比較ToricCode模型與s波超導相的低能激發

3.4拓撲量子相變

ToricCode模型由于其簡單性和豐富性在拓撲序的研究中始終處于核心地位，在任何的拓撲物態探索中都充當著試金石的角色。于是，要研究拓撲序的相變，一個很自然的出發點就是研究該Z2內稟拓撲相的相變。一個最簡單的考慮就是在ToricCode模型中引入外磁場。事實上，與其等價的規范——希格斯理論，早在1979年已經被Fradkin與Shenker所討論。盡管Elitzur定理表明，純粹的規范場其規范對稱性不可自發破缺，但是在與之強耦合的物質場誘導下規范場可以發生破缺，即安德森—希格斯機制。當自旋z方向的磁場hz>>1時，該模型確實發生了希格斯相變，拓撲電荷發生凝聚，系統進入希格斯相，在自旋模型上看即為自旋極化的直積平庸相。而在自旋x方向的磁場hx>>1時，Z2規范場的電場線需要克服的能量正比于其長度，從而拓撲電荷被禁閉，這在自旋模型上看也是自旋極化的直積平庸相。希格斯相與Z2電荷禁閉相通過電磁對偶相聯系，所以該拓撲相變屬于三維伊辛相變的普適類。

從拓撲序的角度看，希格斯相變和電荷禁閉相變分別對應于任意子e與m的凝聚，可作為拓撲序之間相變的任意子凝聚機制的一個典范。目前，已知的任意子凝聚主要指的還是具有玻色型自統計的任意子發生凝聚，比如這里的電荷與磁荷。它與常規的玻色凝聚的區別在于，這類玻色子與其他任意子之間由于Aharonov—Bohm相位效應存在非平庸的統計，從而其凝聚會引發其他任意子的禁閉。在ToricCode模型中，由于磁荷m對電荷e來說充當著π通量的角色，所以磁荷的凝聚會導致電荷的禁閉。直觀的圖像理解是，在磁荷凝聚的基態真空上，磁荷可以任意漲落出現或者消失，而這意味著電荷在真空中游走時會感受到漲落的相位，從而造成干涉相消效應。從邏輯上說，由于電荷在磁荷凝聚的真空中已經不具備良好定義的統計相位，所以不允許獨立存在。同理，電荷的凝聚會導致磁荷的禁閉。

由電磁對偶相聯系的希格斯相與禁閉相，在相圖上被Fradkin和Shenker論證可以絕熱連接。早在1980年，Jongeward等人通過數值計算發現希格斯相與禁閉相之間的電磁對偶線上，在弱場下出現一級相變線，起始于一個臨界點，終結于Z2退禁閉相的邊緣，與希格斯相變線和禁閉相變線交匯在一起，疑似出現一個三相變點。30多年以后，在ToricCode模型提出以后，人們從磁場擾動的角度，以探索拓撲相變為動機又對類似相圖進行了大量探索。一個重要的工作是，在2010年，Tupitsyn，Kitaev，Prokof′ev與Stamp通過將該模型映射到三維經典伊辛模型，并使用大規模蒙特卡羅數值計算的辦法再一次計算了此相圖。然而，其數據仍然無法敲定在疑似三相變點的區域上的情況，如圖9(a)所示。其中最讓人感興趣的是三相變點的可能，盡管這樣的三相變點超越現有的任意子凝聚機制。因為在電磁對偶路徑上，從拓撲相出發，如果發生電荷凝聚，則電磁對偶意味著磁荷也同時發生凝聚。然而由于常規的宏觀凝聚體是玻色性的，所以Aharonov—Bohm效應會阻止電荷凝聚體與磁荷凝聚體的共存。也就是說，狹義的任意子相變機制無法解釋三相變點。因此，盡管圍繞該相圖已經有了可觀的理論與數值的研究，然而在電磁對偶線上的疑似三相變點依舊是未解之謎。自對偶線上的一級相變線和來自希格斯相變與禁閉相變的連續相變線是如何交接？假如是連續的三相變點，那么從拓撲相到非拓撲相的相變機制是什么？任意子命運如何？

圖9(a)擾動ToricCode模型的全局相圖示意。綠點標記無微擾的ToricCode模型的Z2規范退禁閉拓撲相，藍線標記三維伊辛類的拓撲相變，包括電荷凝聚的希格斯相變和電荷禁閉/磁荷凝聚相變。當電磁對偶時，電荷凝聚相與磁荷凝聚相之間出現一級相變線，它起始于一個臨界點上，類似于氣液相變，終結于拓撲相邊界；(b)從拓撲量子態多體波函數獲得的相圖；(c)拓撲量子態多體波函數所對應的經典Ashkin—Teller統計模型的相圖

2019年初，本文作者另辟蹊徑，從嚴格可調節的基態多體波函數的角度，探究了沿著電磁對偶路徑上的可能發生的拓撲相變。這類似于Laughlin寫下的刻畫分數量子霍爾態的多體波函數，只不過我們將其思路推廣到含參數調節的波函數來刻畫一個拓撲量子相變的過程。同樣，類似于Laughlin可將其多體波函數的模方映射到二維經典庫侖等離子體問題論述分數霍爾態的性質，我們發現含參數調節的ToricCode波函數的模方也可以映射到經典Ashkin—Teller統計模型。為此，我們借助于張量網絡態表象，因為張量網絡態可以把一個多體波函數分解為一個個局域的張量的直乘積形式，而局域的張量結構描述的則是物理自由度與某種“糾纏自由度”的耦合。

我們在獲得了波函數模方的張量網絡中，先行將物理自由度縮并掉，而留下“糾纏自由度”，留下的張量網絡對應于一個描述局域相互作用的經典統計模型的配分函數。這種引入輔助自由度解除耦合物理自由度，而后求和掉物理自由度而留下輔助自由度的辦法，精神上類似于在路徑積分上常用的Hubbard—Stratonovich變換。張量網絡態的局域性保證了最終得到的經典模型的局域性。借助Ashkin—Teller模型的嚴格解析解，我們可以確定相變點位置以及任意子關聯函數的標度行為，從而準確地描述相變與相變機制。用這套辦法我們在調節波函數的路徑中重現了電荷凝聚與磁荷凝聚的相變。而在電磁對偶的路徑上，驚奇地發現Z2拓撲相經歷了一個Kosterlitz—Thouless相變進入無能隙的U(1)庫侖氣體相：電荷質量隨著關聯長度發散而逐漸消失，電荷與電荷之間產生與距離成對數依賴關系的二維庫侖勢。其臨界點對應的相變，從庫侖勢的角度看是配對電荷的安德森—希格斯凝聚相變，本質上即為超導相變。借此我們可以推測，在調節ToricCode模型中外磁場所得到的相圖中，沿著電磁對偶路徑上的相變類似于禁閉的U(1)規范場到Z2退禁閉規范場的電荷對凝聚相變，相變的普適類與三維的XY模型等價。具體而言，可以用我們嚴格調節的波函數作為出發點，通過增大張量維數來作為基態擬設，數值求解含有外磁場的ToricCode模型。

此外，非阿貝爾拓撲量子有序態被認為可用于實現拓撲量子計算，而斐波那契拓撲量子態則是實現通用拓撲量子計算最為簡單的物理系統，相關拓撲相變研究在2020年也獲得新進展。利用量子對偶性，我們首先構造了一個含兩個互為對偶且可調的斐波那契拓撲量子態的多體波函數。該波函數的模方可以被映射到一個經典統計配分函數上，我們發現對應的統計模型為兩個二維耦合的

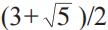
態Potts模型。這是個全新的統計模型，因為它不僅包含了無理數的局域自由度數目，而且還具有非局域的負玻爾茲曼統計因子。此外，通過發展張量網絡的特殊技巧，導出了這個斐波那契拓撲態的張量網絡態表示。借助于張量網絡態的數值計算方法，我們完整而準確地建立斐波那契拓撲物態及其相變的全景相圖，并給出多個拓撲量子相變的臨界性質。

04

結語

值得指出的是，內稟拓撲相的拓撲與此前所介紹的拓撲絕緣體，盡管都統稱為“拓撲量子態”，但是有著非常不一樣的內涵。拓撲絕緣體或拓撲超導體的拓撲往往跟布洛赫態在動量空間中的Berry相位相關，體現在動量空間中具有相對直觀的拓撲結構，比如渦旋或斯格明子。相較而言，內稟拓撲相的拓撲則表觀上體現在演生任意子激發在實空間上相互纏繞的Berry相位因子，其相位因子可以推廣到非阿貝爾的矩陣形式，其背后的物理根源在于低能演生出的拓撲規范場。Kitaev對于內稟拓撲序是根據其核心物理效應和物理刻畫，演生任意子激發定義的。而文小剛則傾向于從微觀的絕熱原理來分類，只要無法絕熱演變成平庸直積態的則定義為拓撲相。在他的理論框架里，拓撲絕緣體和拓撲超導體中的大多數被歸類為對稱保護拓撲相。只要保護對稱性失去，則可以與平庸直積態絕熱相連。而像量子霍爾態并不需要對稱性保護也無法絕熱演變成平庸直積態，但是它們可以通過將兩個相反手征性的體系耦合起來變成平庸態，所以叫作“可逆”(invertible)拓撲相。從波函數的角度，文小剛認為不需要對稱性保護的內稟拓撲相和“可逆”拓撲相的根源都在于長程量子糾纏，數學上由張量范疇理論所描述。

除去分數準粒子激發這樣的宏觀特征之外，量子自旋液體與分數量子霍爾效應更密切的相關性在于手征自旋液體的提出。最早，Kalmeyer與Laughlin通過對阻挫自旋系統作Holstein—Primakoff變換到玻色子體系，發現阻挫相互作用等價于強磁場，從而將自旋液體跟分數量子霍爾效應從微觀上聯系了起來，提出了手征自旋液體。最簡單的Kalmeyer—Laughlin手征自旋液體可以由阿貝爾Chern—Simons拓撲規范場理論來描述，具有Semion統計的準粒子激發。而具有時間反演對稱性的Z2量子自旋液體則需要二分量的相互Chern—Simons作用量，進而描述了兩個相互間具有Semion統計的玻色子準粒子激發。

目前已知的能夠將較多內稟拓撲相聯系起來的相變理論框架是任意子凝聚機制。狹義的任意子凝聚機制又叫“拓撲對稱性破缺”，是將傳統的玻色凝聚建立長程有序的范式推廣到具有玻色型自統計的任意子，伴隨著這種“玻色子”的凝聚，與之有非平庸統計關系的任意子會被禁閉。一個最簡單的例子就是超導渦旋凝聚導致的超導—絕緣體相變。對于更一般的具有非玻色型自統計任意子的凝聚，迄今依舊是極為挑戰性的物理問題。

縱觀凝聚態物理學的發展史，可以發現往往是先從一些具體而又典型的現象個例中獲得突破，進而推而廣之，建立一整座宏偉大廈，可謂“從一、而二、及三、至無窮”。雖然現實世界是三維空間，然而禁閉在低維空間中的凝聚態物理系統，其漲落效應更強，從而更容易演生出新奇的量子物態。而相比起一維系統，二維量子系統鮮有嚴格解，卻又更容易出現在現實的材料系統中，所以成為強關聯多體領域尤受關注而極具挑戰的方向。強關聯電子系統的典型特征是相互作用與電子動能相比擬，甚至遠大于后者，從而能帶論完全失效。一般而言，對這樣的體系沒有普適的嚴格處理辦法，只能通過理論上從不同的角度做近似或者通過大規模數值計算來探知其性質，除了極少數嚴格可解模型。這樣的系統往往具有豐富而新奇的演生量子現象，比如高溫超導、分數量子霍爾效應和量子自旋液體，所以是凝聚態物理學領域一個長盛不衰的研究方向。

致謝衷心感謝于淥先生對本文作者長期從事拓撲量子物態及其相變理論研究的支持和鼓勵。

參考文獻

AndersonPW.Science，1972，177：4047

張廣銘，于淥.物理，2010，8：39

于淥，郝柏林，陳曉松.邊緣奇跡：相變和臨界現象.北京：科學出版社，2005

SachdevS.QuantumPhaseTransitions.CambridgeUniversityPress，1999

KosterlitzJM，ThoulessDJ.JournalofPhysicsC：SolidStatePhysics，1973，7：1181

WenXG.Rev.Mod.Phys.，2017，89：041004

BerryMV.ProceedingsoftheRoyalSocietyofLondon.A.MathematicalandPhysicalSciences，1984，392：45

ThoulessDJ，KohmotoM，NightingaleMPetal.Phys.Rev.Lett.，1982，49：405

HaldaneFDM.Phys.Rev.Lett.，1988，61：2015

KaneCL，MeleEJ.Phys.Rev.Lett.，2005，95：226801

BernevigBA，HughesTL，ZhangSC.Science，2006，314：1757

EzawaM.Phys.Lett.A，2014，16：1180

ChangCZ，ZhangJ，FengXetal.Science，2013，340：167

FuL，KaneCL.Phys.Rev.Lett.，2008，100：096407

ReadN，GreenD.Phys.Rev.B，2000，61：10267

WilczekF.Phys.Rev.Lett.，1982，49：957

NayakC，SimonSH，SternAetal.Rev.Mod.Phys.，2008，80：1083

LaughlinRB.Phys.Rev.Lett.，1983，50：1395

MooreG，ReadN.NuclearPhysicsB，1991，360：362

WittenE.CommunicationsinMathematicalPhysics，1989，121：351

WenXG.InternationalJournalofModernPhysicsB，1990，4：239

VerlindeE.NuclearPhysicsB，1988，300：360

AndersonPW.Science，1987，235：1196

RokhsarDS，KivelsonSA.Phys.Rev.Lett.，1988，61：2376

WenXG.Phys.Rev.B，1991，44：2664

MoessnerR，SondhiSL.Phys.Rev.Lett.，2001，86：1881

KitaevA.AnnalsofPhysics，2003，303：2

LevinMA，WenXG.Phys.Rev.B，2005，71：045110

HanssonT，OganesyanV，SondhiS.AnnalsofPhysics，2004，313：497

FradkinE，ShenkerSH.Phys.Rev.D，1979，19：3682

ElitzurS.Phys.Rev.D，1975，12：3978

BaisFA，SlingerlandJK.Phys.Rev.B，2009，79：045316

JongewardGA，StackJD，JayaprakashC.Phys.Rev.D，1980，21：3360

TupitsynIS，KitaevA，Prokof′evNVetal.Phys.Rev.B，2010，82：085114

ZhuGY，ZhangGM.Phys.Rev.Lett.，2019，122：176401

BaxterRJ.ExactlySolvedModelsinStatisticalMechanics.London：AcademicPress，1982

XuWT，ZhangQ，ZhangGM.Phys.Rev.Lett.，2020，124：130603

KalmeyerV，LaughlinRB.Phys.Rev.B，1989，39：11879

WenXG，WilczekF，ZeeA.Phys.Rev.B，1989，39：11413

BurnellF.AnnualReviewofCondensedMatterPhysics，2018，9：307

本文經授權轉載自微信公眾號“中國物理學會期刊網”。

Tags：TellerTKNBECTeller幣是什么幣TKN幣TKN價格BEC幣BEC價格

酷幣