數字簽名：基于橢圓曲線的簽名方案_數字貨幣:Oscar Bond

在數字時代中，數字化文檔的認證性、完整性和不可否認性，是實現信息化安全的基本要求。數字簽名則是滿足上述要求的主要方式之一，亦是現代密碼學的研究內容之一。

數字簽名有哪些形式？基于密碼學的數字簽名優勢幾何？有哪些常用的數字簽名實現方案？使用過程中又潛藏何等風險？我們將先從理解概念為始，再為大家逐步深入介紹。

區塊鏈百科No.34：基于橢圓曲線簽名方案

隨著計算機信息處理能力的不斷提高，對密鑰長度的要求也越來越高，這個問題對于存儲能力受限的系統來說顯得尤為突出。

橢圓曲線密碼體制（ECC）的提出改變了這種狀況，它可以用更短的密鑰提供與其他體制相當的或者更高級的安全，并已成為迄今被實踐證明安全、有效、應用較廣的3種公鑰密碼體制之一。本文將繼續為大家介紹基于橢圓曲線的數字簽名方案。

時尚科技公司About You推出支持NFT的數字時尚平臺Hypewear:4月15日消息，總部位于德國的時尚科技公司About You宣布推出支持NFT的數字時尚平臺Hypewear，旨在為前衛時尚愛好者和NFT愛好者提供一個數字時尚商店。據悉，Hypewear的未來版本將支持使用歐元和美元進行支付。（Fibre2Fashion）[2022/4/15 14:26:29]

橢圓曲線在代數學和幾何學上，已被廣范研究了150年之久，有堅實的理論基礎。

所謂橢圓曲線是指維爾斯特斯拉（Weierstrass）方程：

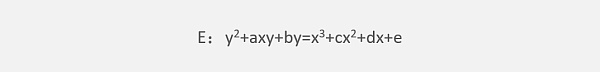
所確定的平面曲線，其中a、b、c、d、e屬于域F，其可以是有理數域Q、復數域C，還可以是有限域GF（p）。

掌柜調查署 | Bondly CEO Brandon：我們的產品能讓用戶只需不到五分鐘就把任何一種數字產品代幣化:在今日舉行的《掌柜調查署 | Bondly重新定義“價值”與“交易”》直播中，針對“傳統托管市場存在哪些問題？Bondly如何改變市場現狀？”的問題，Bondly CEO Brandon表示，通過我個人經驗以及多年體驗線上商品和服務交易的經驗，我注意到傳統托管服務成本高昂且效率低下。當賣方與買方就價格達成協議之后，中間商會收取10％的高額費用，而且賣方優勢可能需要等待10多天才能收到貨款。我們想讓每一個用戶都能使用Bondly的產品進入自己的數字貨幣交易市場，

銷售數字商品和服務的市場潛在價值高達4萬億美元，涉及社交媒體帳戶、網站域名，數字業務等。理論上來說，買賣雙方應該自己掌握交易權力。所以我問自己，為什么現在買賣雙方的交易能力會受到限制？如果交易不是由用戶執行的，那么一定是交易過程存在問題。就在上個月，一個中國抖音賬戶以超過100萬美元的價格售出。去年11月，一個Instagram賬戶以超過8400萬美元的價格售出。這個市場只是剛剛開始增長，但是目前還沒有解決方案來處理這些資產的支付和轉移。我們的產品能讓用戶只需不到五分鐘就把任何一種數字產品代幣化，市場數據庫就能對他們的產品進行估值，并上架需要銷售的產品。賣方可以直接從銷售中獲得收益，無需向傳統托管服務提供商支付各種費用，也避免了其他各種麻煩。[2021/1/5 16:30:20]

橢圓曲線是其上所有點（x、y）的集合，外加一個無窮遠點O（定義橢圓曲線上一個特殊的點，記為O，它為仿射平面無窮遠的點，稱為無窮遠點。在xOy平面上，可以看做平行于y軸的所有直線的集合的一種抽象）。

福州市發布2020年數字福州工作要點，加快打造區塊鏈經濟綜合試驗區:福州市近期發布2020年數字福州工作要點，指出今年福州市將力爭數字經濟規模突破4500億元，努力將福州打造成為全國數字應用第一城和數字中國建設示范城市，打好三年行動計劃“收官戰”。要點指出，加快推動數字經濟新興領域發展。加快打造區塊鏈經濟綜合試驗區，新培育區塊鏈企業30家以上，新增重點行業應用示范20項以上；大力推進工業互聯網建設，力爭全市工業企業“上云上平臺”突破1500家。（新華網）[2020/7/23]

密碼學中普遍采用的是有限域上的橢圓曲線，它是指橢圓曲線方程定義式中，所有的系數都是在某一有限域GF（p）中的元素。它最簡單的公式為：

行情 | 區塊鏈板塊收漲0.56%，數字貨幣板塊收漲0.45%:A股收盤，上證指數收漲0.31%，區塊鏈板塊收漲0.56%，數字貨幣板塊收漲0.45%。區塊鏈板塊中197只概念股中，130只上漲，56只為跌，10只平盤，1只停牌，其中深大通和金冠股份漲停，并無跌停個股；數字貨幣板塊31只概念股中，17只上漲，2只平盤，12只為跌。[2019/12/3]

該橢圓曲線上只有有限個離散點，設為N，則N稱為橢圓曲線的階為N。N越大，安全性越高。基于此，橢圓曲線的圖示可以表示如下：

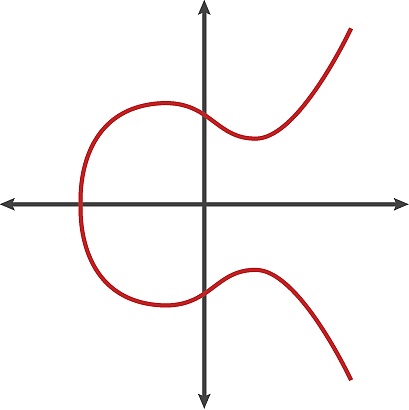
當然，基于不同變量值，橢圓曲線還有其他的表示形式：

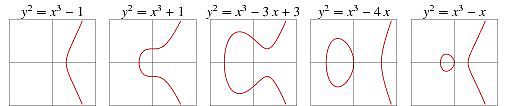
金色相對論 | 朱江：與現有的加密貨幣相比，央行數字貨幣更具有支付的便利性:在今日舉行的金色相對論中，關于“央行數字貨幣和現在討論的加密貨幣有哪些區別”的問題，金山云區塊鏈部門總經理朱江表示，與現有的加密貨幣相比，央行數字貨幣更具有支付的便利性，而加密貨幣更具備匿名性等特點。加密貨幣并不適合做支付，主要原因是不穩定，這兩天的行情大家肯定體會到了。凡是不穩定的都不適合做支付，因為在支付的下一秒價格變了。跟加密貨幣的區別第二個是現鈔M0的替代，而加密貨幣天生是要顛覆中心化貨幣發行方式。現鈔流通有幾個特點，面對面，無需賬戶體系，匿名性等。我也一直在思考如何使用央行發行的數字貨幣，是不是有個電子錢包就可以了，而不需要銀行賬戶。如果電子錢包丟了，那么就好比現金丟了一樣，只能靠失物招領來取回。央行數字貨幣是不是一定是完全留痕的，我認為不一定。[2019/8/15]

當我們仔細觀察這些曲線時，能發現一些有趣特性：（1）對稱性，即曲線上的任何一點都可以在x軸上反射，并保持曲線不變；（2）任何非垂直直線與曲線的交點至多有三個。

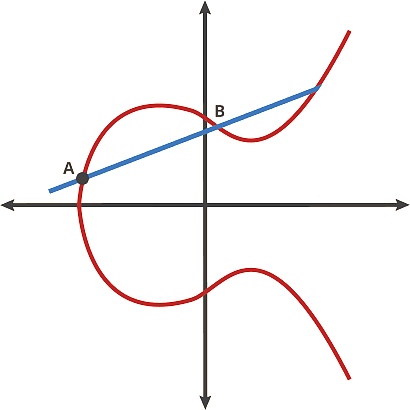
我們可以把這條曲線想象成一場桌球游戲。在曲線上取任意兩點并通過它們畫一條直線，它將與曲線相交于另一個位置。在這個桌球游戲中，你在A點拿一個球，把它射向B點，當它擊中曲線時，球要么直接向上反彈(如果它在x軸以下)，要么直接向下反彈(如果它在x軸以上)到曲線的另一邊。我們可以把球看做在兩個點間移動，曲線上的任意兩點碰撞可得到一個新的點。

A·B = C

或者可以用某一個點自身不斷碰撞出新的點。

A·A = B

A·C = D

……

在這個過程中，一個初始點經由n次運算會得到最后到達的點，當你只知道這兩個點的值，要找出n是很難的。

這就像一個人在房間里隨機玩一段時間桌球游戲，對他而言，按照上面描述的規則一遍又一遍地擊球是很容易的。但如果有人走進房間，球剛好結束到達一個點，即使他知道所有的游戲規則，以及球從哪個點開始，也不能確定球到達此處所被擊中的次數。容易正向計算，難以反向計算，這也是陷門函數的基礎。

1985年，Koblitz和Miller將橢圓曲線引入密碼學，提出了基于有限域GF（p）的橢圓曲線上的點集構成群，在這個群上定義離散對數難題并構造出基于其的一類公鑰密碼體制，即基于橢圓曲線的離散密碼體制，其安全性基于橢圓曲線上離散對數問題的難解性。

我們以基于橢圓曲線的ECDSA數字簽名實現方案為例，闡述其具體的實現過程。

密鑰生成算法

假設GF（p）為有限域，E是有限域GF（p）上的橢圓曲線。選擇E上一點G∈E，G的階為滿足安全要求的素數n，即nG=O（O為無窮遠點）。

選擇一個隨機數d，d∈[1，n-1]，計算Q，使得Q=dG。那么公鑰為（n，Q），私鑰為d。

簽名算法

假設待簽名的消息為m，經過如下計算過程，簽名者對消息m的數字簽名為（r，s）。

驗證算法

簽名接收者B對消息m簽名（r，s）的驗證過程如下：

判斷r和r1的關系，如果相等，則簽名有效；否則，簽名無效。

除了上述介紹ECDSA方案之外，基于橢圓的數字簽名方案還有很多，而類似DSA的其他方案例如Schnorr、EIGamal等方案也都被移植到橢圓曲線有限群上。

從上述介紹可知，數字簽名的安全性依賴于基于橢圓曲線的有限群上的離散對數難題。

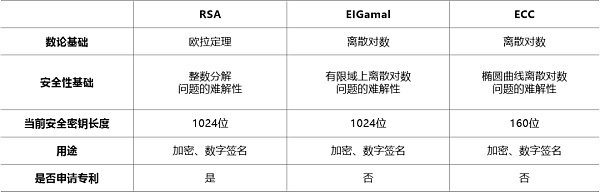
與前章所述RSA數字簽名和基于有限域離散對數的數字簽名相比，基于橢圓曲線的數字簽名方案具有如下特點：在相同的安全強度條件下，簽名長度短，密鑰存儲空間小，適用于存儲空間有限，帶寬受限、要求高速實現的場合。

此外，橢圓曲線資源豐富，同一有限域上存在著大量不同的橢圓曲線，這也為安全性增加了額外的保障。

正是由于橢圓曲線具有豐富的群結構和多選擇性，并可以在保持和RSA、EIGamal體制同樣安全性的前提下大大縮短密鑰長度，因而有著更為廣闊的應用場景。

Tags：數字貨幣區塊鏈加密貨幣BOND數字貨幣交易所開發系統vp幣區塊鏈價格加密貨幣有哪幾種Oscar Bond

以太坊交易