密碼學原語如何應用？解析密碼學特有的數據編解碼_區塊鏈:ripple

作者：廖飛強來源：微眾銀行區塊鏈

隱私保護方案的工程實現，如何關聯到學術論文中天書一般的公式符號？密碼學工程中，有哪些特有的數據編解碼方式、存在哪些認知誤區和注意事項、需要克服哪些限制和挑戰？

作為支撐隱私保護方案的核心技術，如何運用數據編解碼，將密碼學論文中抽象的數學符號和公式具象成業務中具體的隱私數據，是學術成果向產業轉化需要跨過的第一道門檻。

學術論文中所使用的數學語言與工程中所使用的代碼編程語言，差異非常大。不少在數學上容易定義的屬性和過程，若要在工程上提供有效實現，頗具挑戰。實現不當的話，甚至可能破壞學術方案中的安全假設，最終導致方案失效、隱私數據泄露。

常用的密碼學算法擁有多種標準化編解碼方式，其應用到隱私保護方案，可以分別解決相應問題。以下將逐一展開。

1.業務應用難題：類型不匹配，工程實現之道：數據映射

在實際業務中，隱私數據可以表現為五花八門的數據類型，這些類型通常不滿足密碼學協議中特定的類型要求，無法被直接使用，這就是我們需要解決的第一個問題：數據類型不匹配。

例如，業務系統中，交易的金額是一個長整型整數，而常見的密碼學算法可能要求輸入為有限循環群中的一個元素，如果直接使用長整型整數的值，可能該值并不在對應的有限循環群中；在橢圓曲線系統中，單個數值還需要轉化成曲線上的點坐標，需要將一個數值轉化成兩個數值的坐標形式。

IoTeX密碼學負責人：區塊鏈技術可以提高物聯網設備安全性:太平洋時間11月9日，IoTeX密碼學負責人Xinxin Fan博士將在物聯網設備安全會議上向全球數百名與會者分享關于“從區塊鏈技術角度看物聯網設備安全”的主題演講。范博士認為：“區塊鏈技術可以提高物聯網設備安全性，新的Web 3.0機器金融#MachineFi能確保物聯網設備安全的設備身份，數據傳輸和通證化”。IoTeX作為硅谷開源項目成立于2017年，以鏈接現實世界和數字世界為愿景，是與以太坊全兼容的高性能公有區塊鏈。[2021/11/9 6:41:16]

針對以上問題，密碼學工程實現中，一般通過數據映射進行類型轉換處理。具體而言，是將用戶的隱私數據，通過一定的方法，變換到具體密碼協議要求的數據類型。

下面以密碼學中的橢圓曲線(EllipticCurve)加解密為例，介紹一種常見的數據映射方式。橢圓曲線可以簡單理解為定義了一個特定點的集合，例如下面這種公式定義了比較常見的一類橢圓曲線：

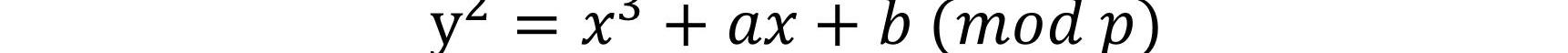
其中滿足公式成立的點(x,y)都在橢圓曲線上。橢圓曲線密碼通過在限定的點集上定義相關的點運算，實現加解密功能。

在橢圓曲線加解密過程中，首先面臨的問題是『如何將待加密的數據嵌入到橢圓曲線上，通過點運算來完成加密操作』。這需要將明文數據m映射到橢圓曲線上的一個特定點M(x,y)。

新理論聲稱密碼學家Len Sassaman是中本聰:一種新的理論聲稱，加密專家和密碼朋克Len Sassaman可能是匿名的比特幣創建者中本聰。在一篇Medium文章中，名為Leung的作者提出了多個原因。首先，在Sassaman于2011年7月3日去世的兩個月前，中本聰發送了他的最終通訊。根據Leung的說法，Sassaman在加入Network Associates協助開發PGP加密時也曾與Hal Finney合作，而Finney是第一個從中本聰處接收比特幣的人。Leung補充說，Sassaman的隱私立場也與導致比特幣網絡被創建的意識形態相吻合。他還指出，在開發比特幣期間，Sassaman居住在比利時，而據報道，在從事該項目時，中本聰居住在歐洲。（dailyhodl）[2021/3/8 18:23:38]

數據編碼方式是將明文數據m通過進制轉換到橢圓曲線上某點的x坐標值，然后計算m^3+am+b的完全平方數，得到y，這樣就將m轉換到了點M(x,y)。

數據解碼方式比較直白，解密還原出明文數據點M之后，讀取M的x坐標值，再通過進制轉換還原為明文信息m。

然而，密碼橢圓曲線是定義在有限域上的，即曲線上是一個離散的點集合。這樣會導致計算完全平方數不一定存在，即x沒有對應的y在橢圓曲線上，那么，部分明文數據無法轉換到橢圓曲線上的點，從而導致部分數據無法被直接加密。

瑞士密碼學家Christian Cachin：Ripple網絡中沒有共識:瑞士密碼學家、伯爾尼大學計算機科學家Christian Cachin在其博客文章“Ripple網絡中沒有共識”中表示，對Ripple協議的技術分析表明，在陳述的假設下，其既不能確保安全，也不能確保其活動性。文章稱，借助其模型可證明，即使在極端溫和的對抗條件下，Ripple的協議也無法達成共識，并且可能妨礙安全性和活力。尤其是，網絡可以在Ripple聲明的UNL重疊的標準條件下，且在只有極小部分的惡意節點的情況下分叉。在網絡忽略或延遲正確節點之間的消息的時間段內，惡意節點可能只是向正確的節點發送沖突消息。其還演示了即使所有節點都具有相同的UNL并且只有一個拜占庭節點，Ripple的共識協議也可能會失去活力。如果發生這種情況，則必須手動重新啟動系統。文章得出結論稱，Ripple網絡的共識協議很脆弱，無法確保計算機科學和區塊鏈從業人員普遍理解的共識。[2020/12/3 22:55:52]

在實際工程化的方案中，為了保證橢圓曲線加解密的可用性，會加入其它更復雜的擴充編碼機制，以應對明文數據轉換失敗的情況。

一般而言，密碼學協議中所定義的類型要求越多，數據映射的工程實現也會越復雜，如果缺乏高效的數據編解碼算法和配套的硬件優化支持，即便密碼學協議的理論計算復雜度再低，最終也是難以實用化。

具體的數據映射涉及到很多流程細節和算法參數，一旦存在微小的差異，由不匹配的編碼算法所產生的數據，都會極大概率無法解碼，導致隱私數據丟失、業務中斷。

聲音 | 迅雷張驍：區塊鏈發展與密碼學的提升密不可分:據洞察網消息，迅雷鏈底層研發工程師張驍表示，區塊鏈之所以能夠解決人與人之間的信任問題，就是因為它的不可篡改性，而這種特性本質上又是基于密碼學算法來實現的。因此密碼學在區塊鏈中的地位很關鍵，區塊鏈作為信任的基石，密碼學則是區塊鏈的基石。

他相信，未來區塊鏈的發展與密碼學在安全領域上的提升是密不可分的，所以迅雷鏈也會緊密地去關注密碼學未來的發展。[2018/12/24]

所以，在具體工程實現時，數據映射需要嚴格按照已有工程標準的實現要求，以國密SM2為例，可以參考GM/T0009-2012《SM2密碼算法使用規范》、GM/T0010-2012《SM2密碼算法加密簽名消息語法規范》等一系列相關技術標準。

2.業務應用難題：數據太長，工程實現之道：數據分組

除了類型不匹配，密碼學協議中使用的核心算法對輸入的數據長度往往也有一定要求。但在實際應用中，需要處理源自不同業務需求的隱私數據，難以限定其長度，難免會出現數據長度超出核心算法處理長度的情況。

例如，對稱加密AES算法AES-128、AES-256，表明其使用的密鑰位數分別是128位和256位，但加密過程中單次進行核心密碼運算時處理的數據固定為128位。

針對以上問題，密碼學工程實現中一般通過數據分組進行處理，即化整為零，將長數據切分為多個較短且符合長度要求的數據塊。

金色財經現場報道 現代密碼學之父：近幾年是密碼學的又一次復興:金色財經現場報道，今日在Coindesk 2018共識會議上，現代密碼學之父，圖靈獎得主，Cryptic Labs首席科學家Whitfield Diffie表示，最近幾年是密碼學的又一次復興，區塊鏈是密碼學方面的重新對焦。他表示喜歡“引入市場力量”的說法， 從市場力量的角度看待密碼學的發展可能是最好的。Diffie還稱贊了比特幣創始人Satoshi，他說：“多年來密碼學領域的許多人都想到如何發展金錢技術，在Satoshi之前沒有人取得成功。”[2018/5/15]

典型的例子是分組加密，例如AES、DES等。分組加密顧名思義就是，將輸入的數據分組為固定長度的數據塊，然后以數據塊為單位作為核心密碼算法的處理單元進行加解密處理。

為了在數據分組之后，依舊保持方案的安全性，數據分組技術不僅僅是簡單地對數據進行劃分，還需要引入額外的流程操作。

下面以AES256位密鑰加密為例，介紹其中典型的分組加密模式ECB、CBC和CTR。

ECB模式(ElectronicCodeBook)

ECB是最簡單的分組加密模式，也是不安全分組模式的典范。

假定有1280位待加密的數據，ECB模式將其平均分為10個128位數據塊。每個數據塊使用相同的密鑰單獨加密生成塊密文，最后塊密文進行串聯生成最終的密文。

ECB模式的加密特點是在相同的明文和密鑰情況下，其密文相同，因此泄露了明文數據與密文數據之間的關聯性，不推薦用于任何隱私保護方案中。

CBC模式(CipherBlockChaining)

CBC模式通過前后數據塊的數據串連避免ECB模式的缺點。

與ECB模式類似，CBC模式中，每個明文塊先與前一個密文塊進行異或后，再進行加密。在這種方法中，每個密文塊都依賴于它前面的所有明文塊。同時，為了保證每個數據密文的隨機性，在第一個塊中需要使用一個隨機的數據塊作為初始化向量IV。

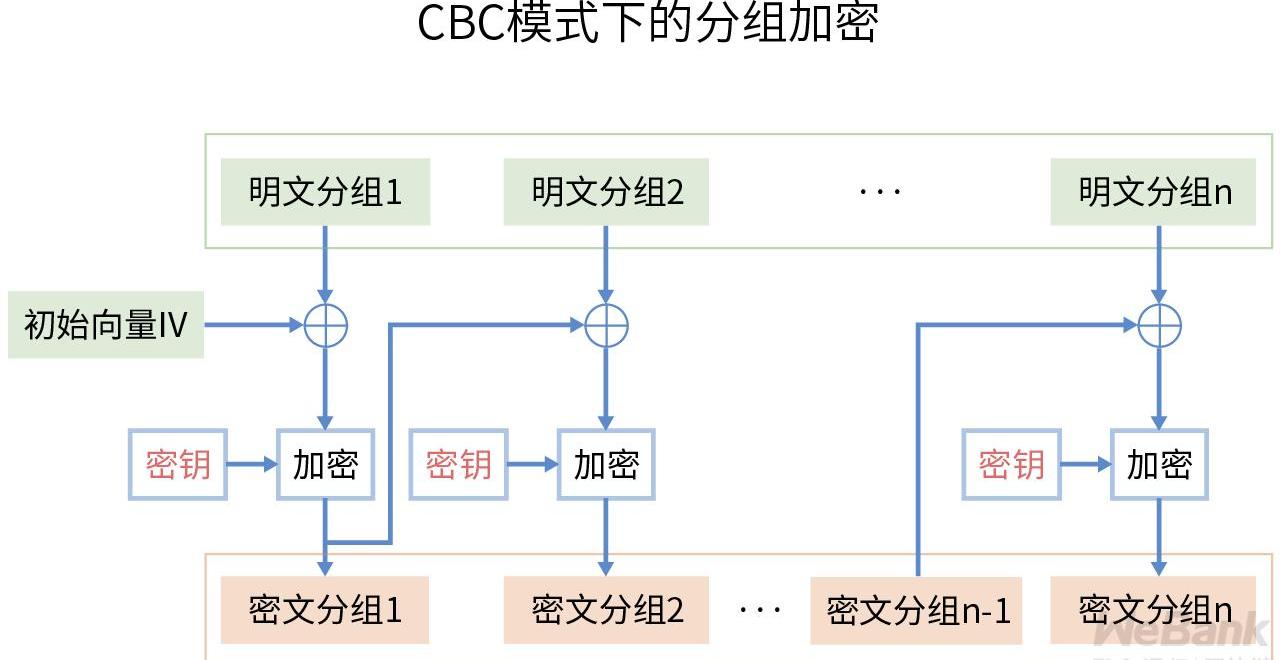
CBC模式解決了ECB模式的安全問題，但也帶來了一定的性能問題。其主要缺點在于每個密文塊都依賴于前面的所有明文塊，導致加密過程是串行的，無法并行化。

CTR模式(CounTeR)

CTR模式的出現讓分組加密更安全且并行化，通過遞增一個加密計數器以產生連續的密鑰流，使得分組密碼變為流密碼進行加密處理，安全性更高。

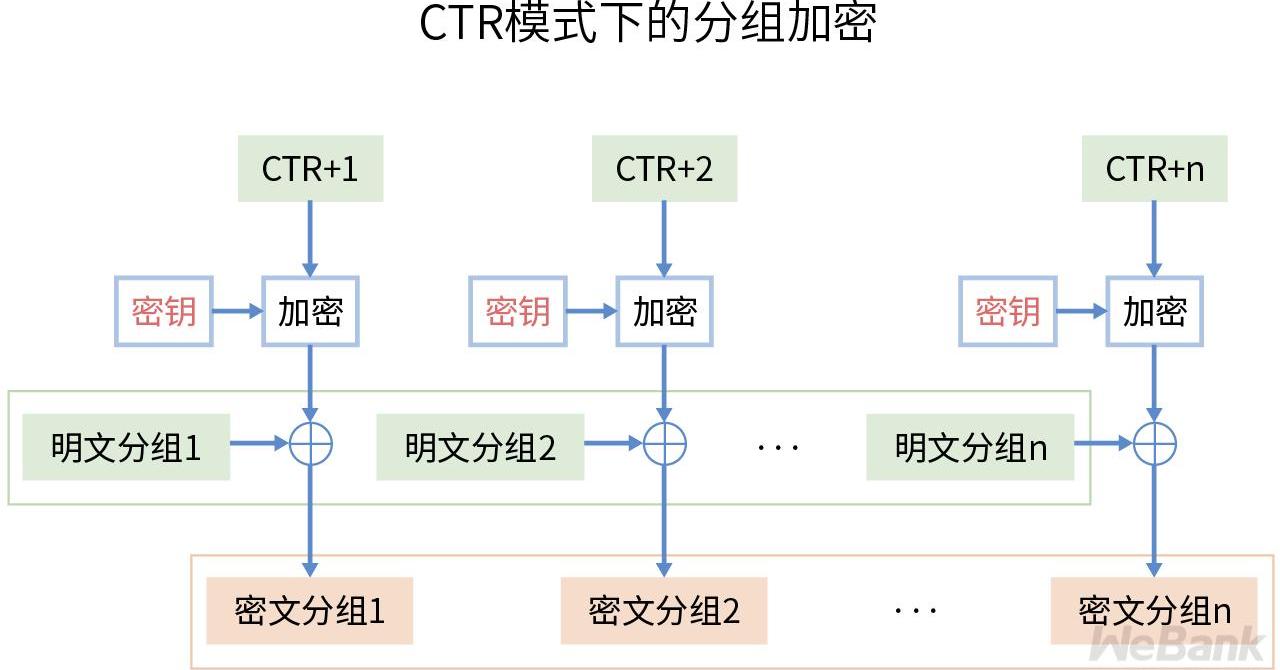
CTR加密和解密過程均可以進行并行處理，使得在多處理器的硬件上實現高性能的海量隱私數據的并發處理成為了可能，這是目前最為推薦的數據分組模式。

密碼學協議中的數據分組與傳統大數據處理中的數據分組有很大區別。理想情況下，數據分組不應該弱化隱私保護的強度，不能為攻擊者獲取未授權的信息提供可乘之機。這往往會涉及精心的數據分組方案設計，不能簡單看作是數據分塊之后的批處理。

3.業務應用難題：數據太短，工程實現之道：數據填充

數據太長是個問題，數據太短往往也是問題。

在以上分組處理的過程中，最后一個數據塊中數據長度不足，密碼學協議中的核心算法也可能無法工作。

假定一個密碼協議處理的數據塊長度要求為6字節，待加密的隱私數據長度為7字節。用兩個十六進制數代表一個字節數據，其示例如下：

b1b2b3b4b5b6b7

7字節長于數據塊的處理長度6字節，因此該數據將被分組，且可以分為兩個數據塊。分組示例如下：

第一個數據塊：b1b2b3b4b5b6

第二個數據塊：b7

其中第一個數據塊剛好是6個字符，第二個數據塊只有1個字節，這個數據塊就太短了，不滿足處理要求。

針對以上問題，密碼學工程實現中一般通過數據填充進行處理，即將短的數據塊填充補位到要求的字節長度。示例中第二個數據塊需要進行數據填充，為其補上缺少的5個字節。

與數據分組類似，這里的數據填充也不是普通的數據填充，也應該滿足一定的安全性要求。最常用的數據填充標準是PKCS#7，也是OpenSSL協議默認采用的數據填充模式。

PKCS#7填充

需要填充的部分都記錄填充的總字節數。應用于示例中第二個數據塊，則補5個字節都是5的數據，其填充效果如下：

b70505050505

這里還存在一個問題：如果一個隱私數據的最后一個分組，剛好就是一個符合其填充規則的數據，在事后提取原始數據時，如何分辨是原始數據還是填充之后的數據？

避開這種歧義情況的關鍵是，任何長度的原始數據，在最后一個數據塊中，都要求進行數據填充。

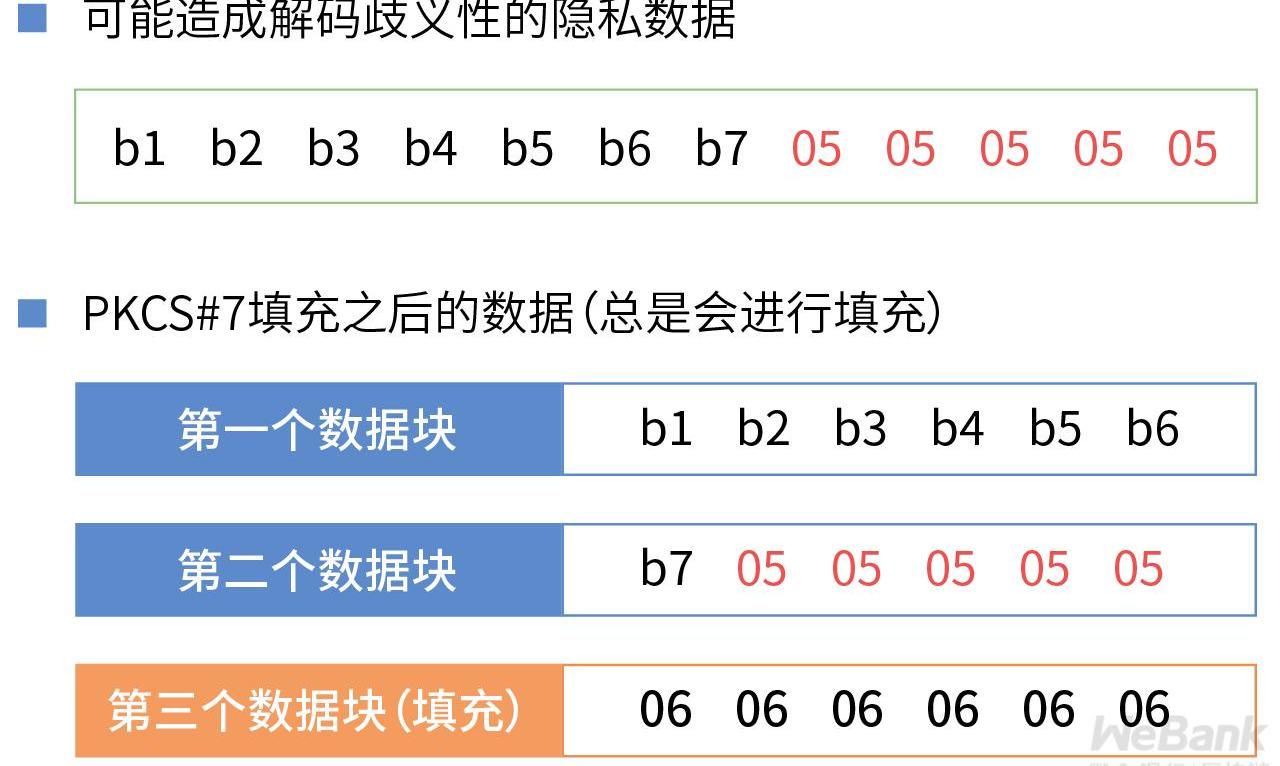
值得注意的是，對隱私數據加密時，按特定填充模式進行處理，那么填充的數據也將被加密，成為加密前明文數據的一部分。解密時，其填充模式也需要和加密時的填充模式相同，這樣才可以正確地剔除填充數據，提取出正確的隱私數據。

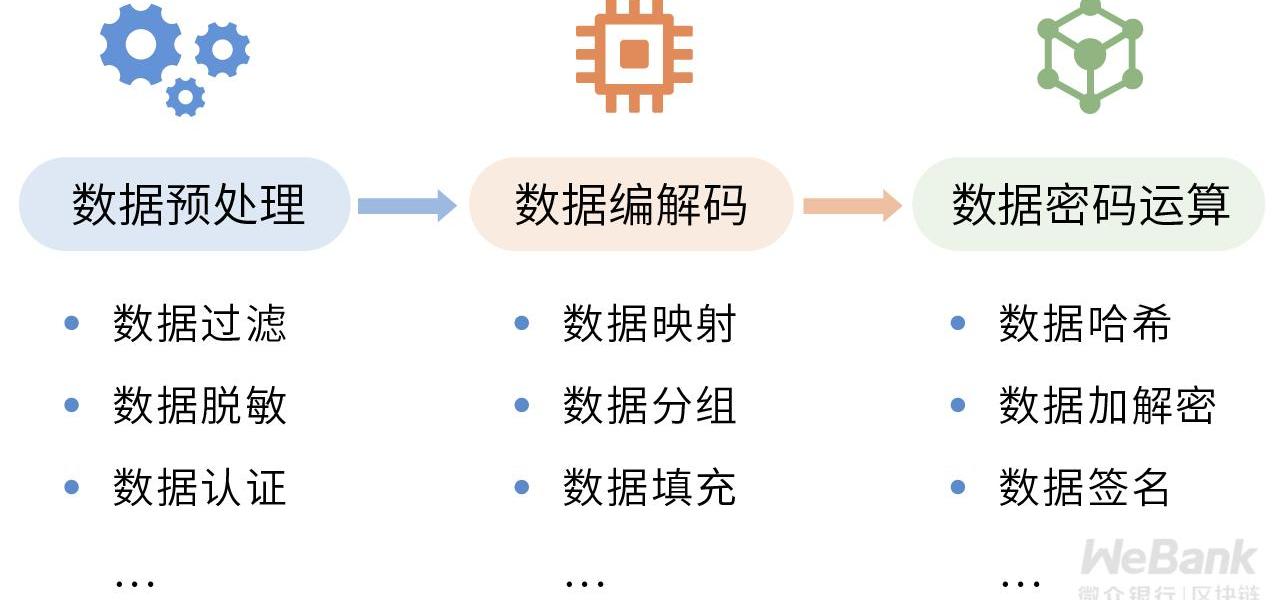
在隱私保護方案的編解碼過程中，以上提到的數據映射、數據分組、數據填充，都是保證隱私數據安全的必要環節。此外，在特定的合規要求下，實際業務系統還需要引入更多的相關數據預處理環節，如數據脫敏、數據認證等，使得數據在進入密碼學協議前，盡早降低潛在的隱私風險。

正是：理論公式抽象賽天書，工程編碼巧手點迷津！

學術論文的公式符號與隱私保護方案的可用工程實現之間，存在一條不小的技術鴻溝，而密碼學特有的數據編解碼，正是我們建立橋梁實現學術成果產業轉化的基石。

安全高效的數據編解碼技術，對于處理以5G、物聯網為爆點的海量隱私數據應用意義重大，是隱私數據進出業務系統的第一道防線，其重要性不亞于其他密碼學原語。

了解完數據編解碼之后，接下來將進入具體應用相關的密碼學原語，欲知詳情，敬請關注下文分解。

————————————————

《隱私保護周三見》

“科技聚焦人性，隱私回歸屬主”，這是微眾銀行區塊鏈團隊推出《隱私保護周三見》深度欄目的愿景與初衷。每周三晚8點，專家團隊將透過欄目和各位一起探尋隱私保護的發展之道。

欄目內容含括以下五大模塊：關鍵概念、法律法規、理論基礎、技術剖析和案例分享，如您有好的建議或者想學習的內容，歡迎隨時提出。

欄目支持單位：零壹財經、陀螺財經、巴比特、火訊財經、火星財經、價值在線、鏈客社區

Tags：區塊鏈ECBripplePPL區塊鏈域名成交ECB價格ripple幣fbaKepple

酷幣下載